Exploring Cardiac Electrophysiology
|
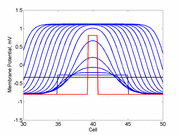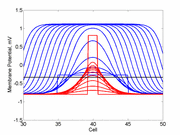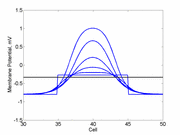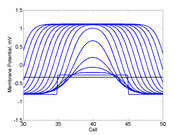
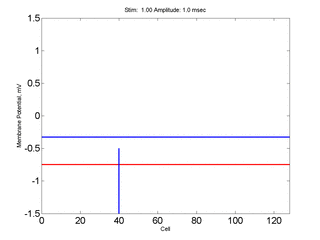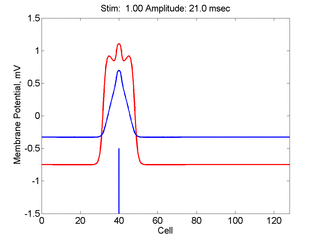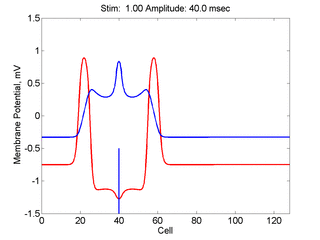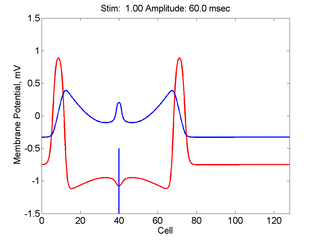 Here,
excitation activates a region larger than the critical nucleus.
Since the medium is uniformly excitable, the
critical nucleus expands away from the point of stimulation resulting
in bidirectional propagation. The excitability is represented by the
blue trace and the red trace is the membrane potential.
Here,
excitation activates a region larger than the critical nucleus.
Since the medium is uniformly excitable, the
critical nucleus expands away from the point of stimulation resulting
in bidirectional propagation. The excitability is represented by the
blue trace and the red trace is the membrane potential.
|
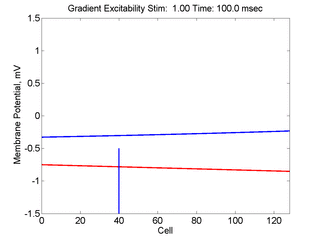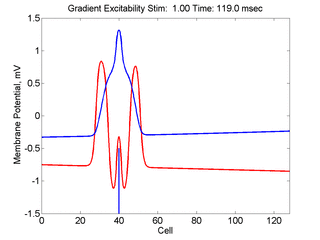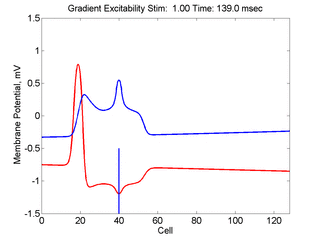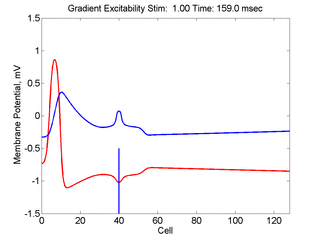 In this case, the inhibitory current (blue)
has a gradient so that the excitability
varies linearly along the cable (grad = 0.001). When
medium is disturbed such that the critical nucleus requirement is exceeded
in the more excitable direction but not met in the less excitable direction,
unidirectional propagation results.
In this case, the inhibitory current (blue)
has a gradient so that the excitability
varies linearly along the cable (grad = 0.001). When
medium is disturbed such that the critical nucleus requirement is exceeded
in the more excitable direction but not met in the less excitable direction,
unidirectional propagation results.
|
The usual situation in cardiac tissue is that as a normal activation wave propagates, it is followed by a recovery region which exhibits a gradient of excitability. The concept of a vulnerable period can be visualized as follows. The vulnerable period represents the time required for a critical excitability point to pass through the excitation field.
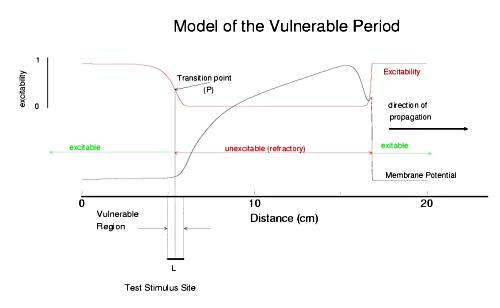
Shown above is a cable with an action potential propagating from left to right. The excitabilty is plotted in red. Rested medium is fully excitable (i.e. the medium in front of the wavefront), while medium within the action potential is fully refractory. Following repolarization of the action potential, the medium recovers its excitability. There is a transition point, P, somewhere between inexcitable and excitable that marks the point where stimlulation results in failed antegrade propagation and successful retrograde propagation. The time require for this point to pass through the stimulation field defines the period of vulnerability and in this case is L/v where L is the width of the stimulus field and v is the propagation velocity of the conditioning action potential. From this simply analysis, one immediately sees that any drug that reduces excitabilty will at the same time, increase the duration of the vulnerable period since wave velocity decreses with decreasing excitabilty (i.e. tissue with reduced excitability requires longer to bring to threshold than tissue of normal excitability).
One of the first descriptions of vulnerability and arrhythmogenic properties of muscle was contained in the work of Mayer (in jelly fish muscle) and Mines and Garrey (in cardiac tissue) where they described the ability to initiate a self-maintained wave of excitation around a ring of excitable tissue. Although this work was done during the early part of this century, the basic ideas expressed with respect to initiation of a reentrant arrhythmia (a pattern of excitation that circulates around either a structural or functional obstacle) are still accepted today.
I got into this drama when I started working in Henry McIntosh's cath lab at Duke. He was concerned about connecting multiple powerline operated devices to a patient and the potential for small leakage currents to initiate ventricular fibrillation. Because catheters were being inserted into the heart and pacemakers were mostly powerline operated, this was a serious concern.
- Mayer, A.G. 1908. The cause of pulsation. The Popular Science Monthly, December 1908: 481-487.
- Mines, G.P. 1913. On dynamic equilibrium in the heart. J. Physiol. (London) 46:349-383.
- Garrey, W.E. 1914. The nature of fibrillary contraction of the heart. Its relation to tissue mass and form. Amer. J. Physiol. 33:397-414.
- Wiggers, C.F. and Wegria, R. 1939. Ventricular fibrillation due to single localized induction in condenser shock supplied during the vulnerable phase of ventricular systole. Am. J. Physiol 128:500-505.
- Starmer, C.F., Whalen, R.E. and McIntosh, H.D. 1964. Hazards of electric shock in Cardiology. American J. Cardiology 14:537-546.
- Nolasco, J.B. and Dahlen, R.W. 1968. A graphic method for the study of alternation in cardiac action potentials. J. Appl. Physiology. 24:191-196
- Starmer, C.F. and Whalen, R.E. 1973. Current density and electrically induced ventricular fibrillation. Medical Instrumentation 7:158-161
From Theory to Experiments: Insights from Krinsky's Program in Pushchino

Until the mid 80s, most of us (in the US and Europe) were pretty well isolated from awareness of the Soviet investigations into wave motion in an excitable medium. Winfree met Zhabotinsky in Prague during July-August, 1968 during a symposium. By a mechanism not known to me, he managed to master the recipe for the Belousov-Zhabotinsky reagent in his lab in the US and demonstrate wave motion in a chemical medium. This brought to the west, a new tool for exploring the properties of an excitable medium - in this case, a chemical excitable medium. Krinsky had earlier observed the similarities between wave motion in the BZ reagent and cardiac arrhythmias - and this set the stage for a two pronged attack on problems of wave formation, fractionation, vulnerability and spiral evolution.

At about the same time, Krinsky was busy establishing a laboratory in Pushchino, a new science city 100 km south of Moscow, on the banks of the river Oka.

As a conservationist, ahead of his time, he unsuccessfuly lobbied for the planting of fruit trees in the space between flat buildings. Today this is still an empty space (see below left).

Its a pity that during summer, we cannot walk out into this open field and enjoy an freshly picked apple or pear.
With a bright group of students and collaborators, he attacked the questions of wave motion in an excitable medium, extended it to cardiac tissue and arrhythmias. Valentin focused attention on the generic properties of an excitable medium and was able to demonstrate thresholding, wave motion and spiral formation with the simple models of Fitzhugh and Naguma. Many of the reports from Pushchino predate reports of similar observations from the US and Europe. In 1986, Valentin Krinsky, Sasha Medvinsky and Sasha Panfilov consolidated much of the Pushchino work into a small booklet as part of a series entitled
- Krinsky, V.I, Medvinsky, A.B. and Panfilov, A. V. 1986. Mathematical Cybernetics (Mathematika Kibernetika) (in Russian)
In 1987, I was invited to the All Union Center for Clinical and Experimental Cardiology in Moscow (Leo Rosenshtraukh's laboratory) in order to explore using the guarded receptor paradigm to characterize several Soviet antiarrhythmic drugs. This led to intense interactions with Adas Undravinos, Nail Burnishev, Ilya Fliedervich, Slava Nesterenko, Vika Bolotina, Boris Khodorov and Valentin Krinsky.

- Krinsky, V.I. 1966. Spread of excitation in an inhomogeneous medium (state similar to cardiac fibrillation). Biofizika. 11:676-683.
- Winfree, A.T. Spiral waves of chemical activity Science 175:634-646, 1972.
- FitzHugh, R. 1961. Impulses and physiologic states in theoretical models of nerve membrane. Biophysical J. 1:445-466.
- Rinzel, J. Excitation dynamics: insights from simplified membrane models. Fed. Proc. 44:2944-2946, 1985
- Starmer, C.F., Undrovinas, I.A., Scamps., F., Vassort, G., Nesterenko, V.V. and Rosenshtraukh, L.V. Ethacizin blockade of Ca++ channels: A test of the guarded receptor hypothesis. Amer. J. Physiol 257:H1693-H1704, 1989.
- Undrovinas, A.I, Burnashev, N., Eroshenko, D., Fleidervish, I., Starmer, C.F., Makielski, J.C. and Rosenshtraukh, L. Quinidine blocks adenosine 5'-triphosphate-sensitive potassium channels in heart. Amer. J. Physiol. 259:H1609-1612, 1990.
- Gomez-Gesteira, M, Fernandex-Garcia, G., Munuzuri, A.P., Perez-Munuzuri, V., Krinsky, V.I., Starmer, C.F. and Perez-Villar, V. Spiral formation in a Belousov-Zhabotinsky medium by premature reexcitation: vulnerability. Int. J. Bifurcations and Chaos 4:1193-1204, 1994.
- Gomez-Gersteira, M., Fernandex-Garcia, G., Munuzuri, A.P., Perez-Munuzuri, V., Krinsky, V.I., Starmer,.C.F. and Perez-Viller, V. Vulnerability in an excitable Belousov-Zhabotinsky medium: from 1D to 2D. Physica D 76:359-368, 1994.
- Aliev, R. R. Heart Tissue Simulations by Means of Chemical Excitable Media. Chaos, Solitons and Fractals 5(3,4), 567-574 (1995).
- Aliev, R. R. and Panfilov, A. V. Multiple responses at the boundaries of the vulnerable window in the Belousov-Zhabotinsky reaction. Phys. Rev. E 52(3), 2287-2293 (1995).
First Description of a Spiral Wave: An Axiomatic Approach for understanding Vulnerability
An early, axiomatic approach to describing the properties of an excitable media was published just after the 2nd world war by the MIT mathematician, Norbert Wiener, with his colleague, A. Rosenblueth. This manuscript provided a superb example of organizing the approach to excitable media by first stating a series of postulates or assumptions. From this work, the concept of vulnerability, i.e. the ability to initiate a unidirectionally propagated wave, was postulated as well as the existance of spiral waves (although limited to the case of a fixed obstacle). Although very little of contemporary literature in computational biology refers to this paper, it, as well as the Rushton and Kolmogorov papers are essential reading for any serious worker exploring wave formation in an excitable medium.
- Wiener, N. and Rosenblueth, A. 1946. The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Archives of the Institue of Cardiology, Mexico, 16:205-265.
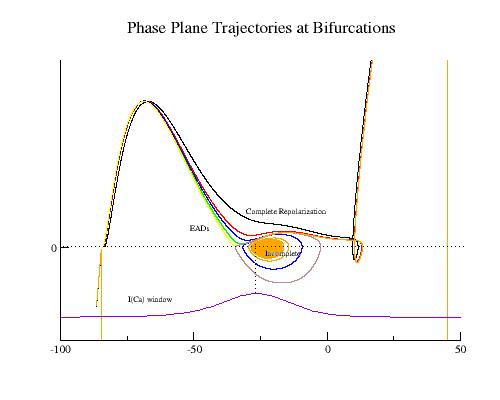
Arrhythmic Mechanisms: The Vulnerable Period and Drug-linked Prolongation of the Vulnerable Period
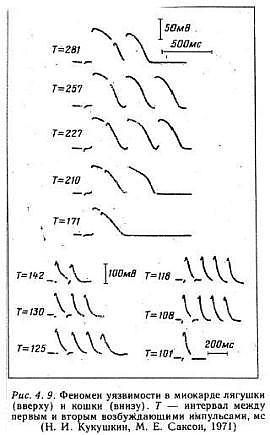
An interesting aspect of studies of excitable media, particularly spiral wave behavior, is that initial attention was focused on the behavior of the waves and their interaction with inexcitable boundaries. With the exception of Kukushkin (who lives down the hall from Krinsky old lab at the Institute of Theoretical and Experimental Biophysics, Pushchino, Russia) it seems only a few were interested in how spiral waves could be initiated. Kukushkin was the first to demonstrate that reentry (sprial wave processes in cardiac tissue) could be initiated by introducing a stimulating pulse during a period of vulnerability which was published in 1971. It was not until I started working with Krinsky and his group that the concept of vulnerability was formalized. This formalization led to new insights into how drugs that were supposed to control cardiac rhythm disturbances could, in fact, promote reentry and lead to sudden cardiac death.
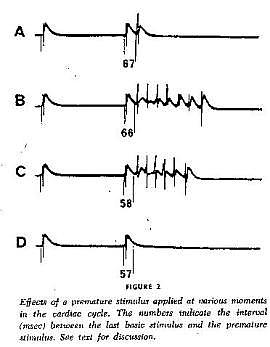
With a conditioning wave triggered by an s1 stimulation and s2 test stimuli, Kukushkin (left), Allessie (right) demonstrated the vulnerable period in frog, cat and rabbit cardiac tissue.
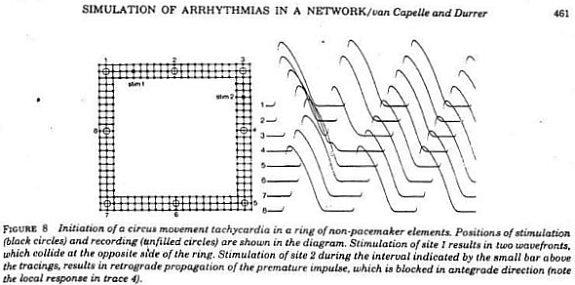
Using a FHN-like model, vanCapelle and Durrer also demonstrated the period of vulnerability in a ring model using s1-s2 stimuli. It was only later, that it was realized that the central "obstacle" was unnecessary to initiate reentry. In the figure below, there is a small bar about 2 cm under the "E" in NETWORK that represents the period of vulnerability.
- Mayer, A.G. 1908. The cause of pulsation. The Popular Science Monthly, December 1908: 481-487.
- Kukushkin, N.I. and Sakson, M.E. 1971. Prediction of the vulnerability of the ventricle to arrhythmia from latency and duration of extrasystolic response. Biofizika, 16:904-909.
- Sakson, M.Y., Kukushkin, N.I. and Bukauskas, F.F. Retrograde excitation in the myocardium and its role in the genesis of arrhythmias of the vulnerable period. Bifizika 17:856-861, 1972.
- Allessie, M.A., Bonke, F.I.M., and Schopman, F.J.G: 1973. Circus movement in rabbit atrial muscle as a mechanism of tachycardia. Circ. Res. 33:54-62.
- Starmer, C.F., Lastra, A.A., Nesterenko, V.V. and Grant, A.O. 1991. A proarrhythmic response to sodium channel blocakde: theoretical model and numerical experiments. Circulation 84:1364-1377.
- Starmer, C.F., Lancaster, A.R., Lastra, A.A. and Grant. A.O. 1992. Cardiac instability amplified by use-dependent Na channel blockade. American Journal of Physiology 262:H1305-H1310.
- Starmer, C.F., Biktashev, V.N., Romashko, D.N., Stepanov, M.R., Makarova, O.N. and Krinsky, V.I. 1993. Vulnerability in homogeneous excitable media: Analytical and numerical studies of unidirectional propagation, Biophysical Journal, 65:1775-1787.
- Starobin, J., Zilberter, Y.I. and Starmer, C.F. 1994. Vulnerability in one-dimensional excitable media. Physica D. 70:321-341.
- Starmer, C.F., Romashko, D.N., Reddy, R.S., Zilberter, Y.I., Starobin, J., Grant, A.O. and Krinsky, V.I. A proarrhythmic response to potassium channel blockade: Numerical studies of polymorphic tachyarrhythmias. Circulation 92:595-605, 1995.
- Spach, M.S. and Starmer, C.F. Altering the topology of gap junctions in nonuniform anisotropy: A major therapeutic target in atrial fribrillation. Cardiovascular Research 30:337-344, 1995.
- Starobin, J., Zilberter, Y.I., Rusnak, E.M. and Starmer, C.F. Wavelet formation in excitable cardiac tissue: The role of wavefront-obstacle interactions in initiating high frequency fibrillatory-like arrhythmias. Biophysical J. 70:581-594, 1996.
- Starmer, C.F. and Starobin, J. Spiral tip movement: The role of repolarizing currents in polymorphic cardiac arrhythmias. Int. J. Chaos and Bifurcations. 6:1909-1923, 1996
- Starmer, C.F. The cardiac vulnerable period and reentrant arrhythmias: Targets of anti- and proarrhythmic processes. PACE 20(part2): 445-454, 1997.
My early career at Duke focused on electric shock hazards and the threshold of ventricular fibrillation in man. The problem was quite interesting, in that 2 second stimulation with 60 Hz current would induce ventricular fibrillation in dogs with currents as low as 16 microamps and in humans with currents as low as 150 microamps. With single DC pulses, the threshold was typically several milliamps. Andy Wallace and his fellows explored both mechanisms and determined that the current threshold was successively reduced with each induced premature impulse. So after one PVC, the threshold of VF was less than after 0 PVCs. Similarly, the threshold after 2 PVCs was less than that following a single PVC. Today, this fits quite will with our view (VP approximately = L/v ) - it is well known tht the propagation velocity following a PVC is less than that of a wave traveling in fully rested medium. See
- Sugimoto, T., Schaal, S.F. and Wallace, A.G. Factors determining vulnerability to ventricular fibrillation induced by 60-CPS alternating current. Circulation Res 221:601-608, 1967.
Pulling all this together, below are some demonstrations of the variety of responses available for premature excitation in a 2D homogeneous medium.
Here we utilize the FHN model. The distance between the front associated with the conditioning wave and the response to the second stimulation (indicated by a black line). The geometric distance associated with a stimulus that falls within the vulnerable period (42 pixels in this example) is between that associated with a decaying response (refractory, 39 pixels) and complete excitation (45 pixels). The length of the vulnerable period in this model is only a few pixels. The left panel represents stimulation within the refractory interval, the right represents stimulation in excitable medium and the bottom panel demonstrates the results from stimulating within the vulnerable region.
The responses to excitation within the vulnerable region also is sensitive to the size of the excitation region as shown here. We vary the length of the s2 excited region - and as you will see, when the region is less than the liminal region, there is no propagated response. When the s2 excited region is > liminal length, then 1, 2 or an infinite number of reactivations are possible as shown here depending on the distance separating the wavelet endpoints. This displays that in addition to a > liminal region, there must be adequate wavelet length such that when the ends curl - they avoid collisions. Under these conditions, the resulting counter rotating spirals will continue to rotate forever.
Monomorphic or Polymorphic Reentry?
A premature impulse falling within the vulnerable region is required to create a wave fragment. Once the wave fragment is created, what is its destiny? If the fragment is less than the liminal region, then it will collapse. If it is greater than the liminal region, then it will evolve, and with enough space, will curve at the end points forming a pair of counter rotating spirals.
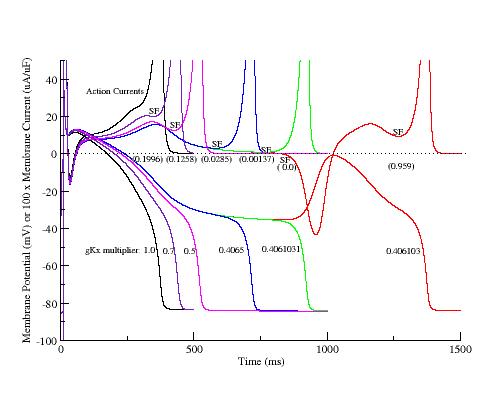
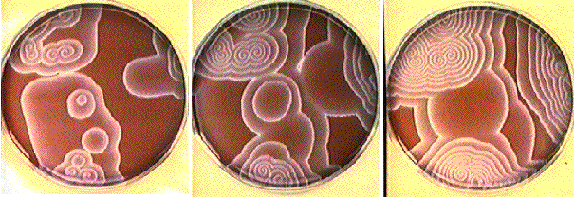
In a homogeneous region, the spiral tips will either rotate about a circular core or they will meander and paint flower-like patterns. Computing the ECG will reveal that a circular core produces a monomorphic ECG while meandering will produce a polymorphic core. The distiction, from our explorations, depends on the magnitude of the inward current available to extend the wave (propagation). If the available inward current is small, then the tip of the spiral can only excite a small region at the tip leading to small curvature of the front. On the other hand, if the available inward current is larger, a larger region is excited at the tip and the curvature as well as velocity are increased. This is best demonstrated with the simple Beeler Reuter model.
How is this related to clinical arrhythmias. The majority of clincial studies implicate reduced potassium currents as a parter in polymorphic reentry. Clearly, reduced K currents at the moment of activation of the sodium current will produce a net increase in I(Na). Similarly in patients with inducible polymorphic VT, a reduction in sodium current (with use-dependent Na blockade) leads to inducible monomorphic VT only.
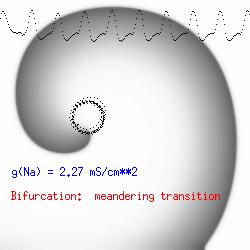
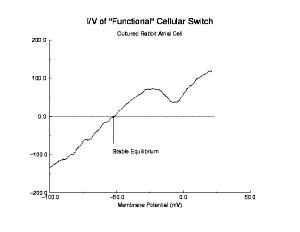
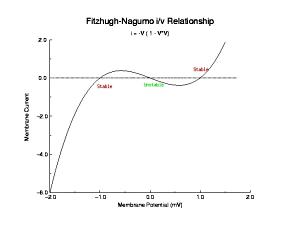
This is the crux of any model of cardiac cells - that there is a continuous fight between sources of an inward current and sources of an outward current that produce a net current. Combined with the cubic-like current voltage relationship seen in BZ, cardiac, Hodgkin-Huxley nerve models and the Fitzhugh-Nagumo abstraction, all these models demonstrate the capacity to make spiral waves. Below we combine the 2d visuals with an approximation of the ECG demonstrating a link between monomorphic ECGs and a non-meandering spiral wave and a polymorphic ECG and a meandering spiral wave. The transition from one to the other is easily produced by simply increasing or decreasing the Na or K currents - either will do the trick because it is the net current that determines whether the spiral meanders or not. Here we show a non-meandering spiral computed from a more complex and biologically realistic model (Beeler-Reuter cardiac cell) Click image for mpeg video : Note that as the sodium conductance is increased from 2.1 mS/cm^2, the diameter of the spiral core decreases until a transition to meandering occurs at 2.27 mS/cm^2. Further increases in gNa increase the degree of meandering as seen below.
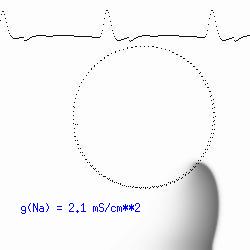
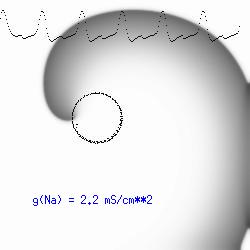

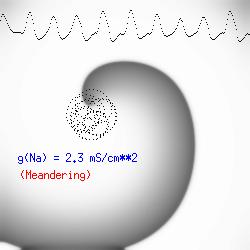
The dotted line reflects the trajectory followed by the tip of the spiral and this trajectory influences the features of the electrocardiogram. Note that increasing the conductance from 2.1 to 2.7 mS reduced the diameter of the tip trajectory as seen above and increases the variability in the individual "QRS" complexes - from monomorphic (gna = 2.1) to polymorphic (gna = 2.3).
A additional small increment in the Na channel conductance which increases the available charge in the front can force a transition to a meandering spiral wave (only a 2% increase) which is the result of the wave tip trying to excite a region less than the liminal threshold (exceeds the maximum curvature defined by the liminal length criteria): To increase the degree of meandering, we increase again the Na conductance (or decrease the K channel conductance as is often accomplished with Class III antiarryhythmic drugs). The physics behind meandering and spiral formation is contained in a series of papers Josef Starobin and I published in the Biophysical Journal, 70:581-594, 1996; (Wavelet formation in excitable cardiac tissue: The role of wavefront-obstacle interactions in initiating high frequency fibrillatory-like arrhythmias); Physica D: 70:321-341, 1994 (Vulnerability in one-dimensional excitable media) and Phys Rev E: 54:430-437,1996 (Boundary-layer analysis of waves propagating in an excitable medium: Medium conditions for wave-front -- obstacle separation); In the following manuscript, we used our boundary layer analysis to predict the transition from circular tip trajectories to meandering and provided some theoretical meat to Art Winfree's elegant numerical experiments where he probed the excitable medium flower garden. Phys Rev E 55:1193-1197, 1997 (A common mechanism links spiral wave meandering and wavefront-obstacle separation), and Phys Rev E 56:3757-3760, 1997 (Boundary-layer analysis of a spiral wave core: Spiral core radius and conditions for tip separation from the boundary).
Vulnerability in Electronic Circuits
I had the good fortune of spending the 77-78 academic year with Jerry Cox and Charlie Molnar at Washington University, St. Louis. During this time, Charlie exposed me to his thinking about asynchronous computing and the challenges of synchronizing two asynchronous processes.
It occurred to me that the glitch, observed in D-type flip-flop circuits, a condition caused by violating the set up time requirments of the clock and data signals, was qualitatively similar to the cardiac vulnerable period. For those interested in the exploring this link here is the 1973 landmark paper published by Charlie and Tom Chaney:
- Chaney, T.J. and Molnar, C.E. 1973. Anomalous behavior of synchronizer and arbiter circuits. IEEE Trans. Comp. pages 421-422
The unstable behavior is clearly shown here with two different circuits. Flip flops operate in either the 0 or 1 state and have a threshold for switching from 1 to 0 and a threshold for switching between 0 and 1. These threshold are different, giving a window potential where the behavior of the flip flop is uncertain. When clock is switched before the data has been asserted for a critical time known as the setup time, then there is inadequate charge accumulated to force the flip-flop to the appropriate state. Consequently the circuit enters a meta-stable state where it can hang around for an undetermined length of time. This metastable state is similar to that seen with near liminal condition stimulation. Shown below are two traces associated with switching the data and clock signals at the same time - from the one state and from the zero state. Note that the potential enters a sort of never-never land where it must decide which bifurcation path to follow. While in the metastable state, downstream logic will see a state that could be interpreted as a one or could be interpreted as a zero. It makes a big problem.
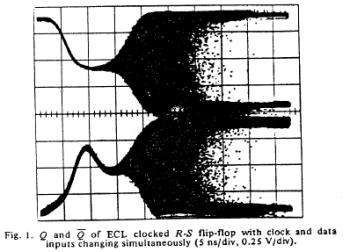
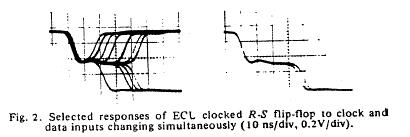
Here they displayed data demonstrating that it was physically impossible to reliably synchronize two asynchronous processes. Coupling the two will be a data line driven by one process and a clock line driven by the other process. Since there is no way to guarantee that the setup constraints (time required for the data to be asserted before it is clocked into the circuit), then there will be an ocassional synchronizer failure.
Abstractly, a cardiac and nerve cell is like a switch - it has two states and it switches back and forth depending on external excitation or an internal oscillatory process. Thus, a computer synchronizer failure is an instance of a computational arrhythmia or more accurately a computation dysrhythmia where the coupling from time to time fails.
It would be interesting to establish some sort of mathematical proof that where there is a switch, there is vulnerability. I can see the support clearly in my mental images of switches and cardiac cells - but I'm not sure how to make a proof.
Anisotropic Connectivity: Initiating spiral waves from identical s1 and s2 sites by varying the stimulus region (or amplitude)
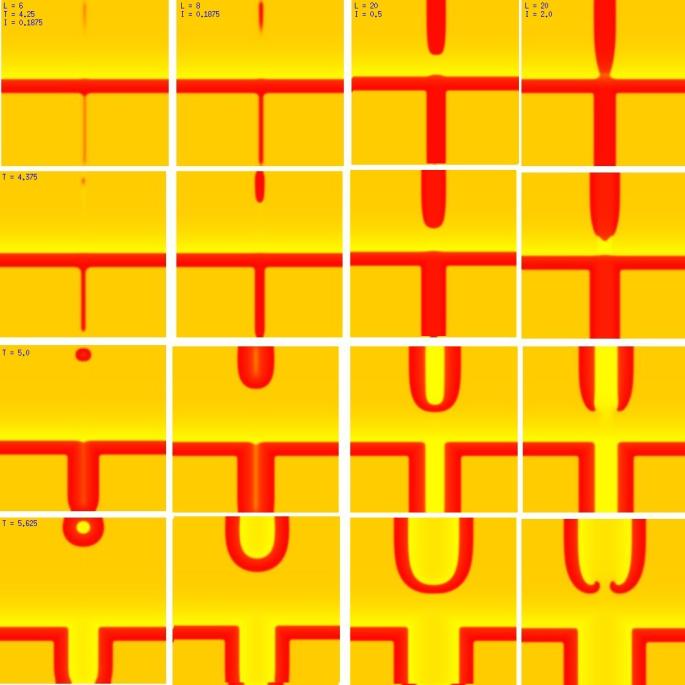
One of the puzzling aspects of starting spirals in cardiac tissue is that it is usually accomplished with two consecutive stimuli arising from the same point. The question of whether one could initiate a spiral in a spiral wave in a medium with identical cells has not been addressed (to my knowledge). Since we know that an asymmetry of excitability is required for wave fragment formation, I hypothesized that we could achieve the requisite asymmetry by implementing anisotropic coupling between cells. The simplest type of anisotropy is uniform anisotropy, discussed by Maddy Spach in his papers on discontinuous propagation. The main idea is that following excitation, the wave will propagate more rapidly in one direction than in an different (perhaps orthogonal) direction. Thus, the medium in the direction of slow conduction will be less excitable than the medium in the direction of fast conduction. Below are the results of 4:1 ratio of longitudinal:transverse coupling between cells. As shown below - this readily creates a vulnerable region within which stimulation can initiate spirals. Shown are 3 electrode lengths - the left, L = 7 dx and results in a decaying front (L < liminal length). The middle panel has L = 8 dx, producing a single reentrant iteration. After the first collision, the remaining fragment is < liminal region and so it collapses. The right panel, L = 9 dx and produces continuous spirals. Look at these new results and enjoy.
The liminal region, illustrated above, is the minimal excited region from which a propagating front can arise. In 2D excitation, with rectangular regions and show below, one can initiate a variety of spiral configurations - depending on which fronts (lateral or longitudinal) survive. Here, on the left, is a small excited region (L = 38 dx) from which only the longitudinal (up-down) fronts survive. On the right, is a larger excited region (L = 50 dx) from which both the longitudinal and transverse fronts survive. Step carefully through each frame and at frame 38, you'll see the separation of the fronts, and either decay or extension of the transverse fronts.
Wave splitting and the lower limit of vulnerability
Shown here is a conditioning wave that propagates from top to bottom - and a stimulus site where the width of the s2 electrode and the amplitude of the stimulus are varied. All frames (horizontally) are aligned in time and indicated in the upper left corner is the width of the electorde (x dimension) as well as the stimulus amplitude. Note that on the left, the amplitude is small as well as the electrode size are small, and only a small region far from the conditioning front is ignited. The 2nd column reveals the responses for a slightly larger (8 dx) electrode. In this case, a target wave is formed because the gradient of excitability is so small that antegrade wave formation is possible. Increasing the stimulus current to 0.5 results in a larger impulse, igniting closer to the conditioning wave, but still only a target wave forms. Note that a bridge forms that joins the fronts that propagate to the left and right respectively. It is this bridge that must be destroyed if the target is to fail and spiral evolution is to occur. Finally, with a large current, the ignited region impact two spirals evolve from the 2 wave fragments.
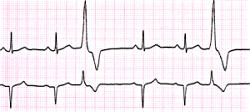
Ventricular Fibrillation and the Vulnerable Period
One interesting side note relates to the origin of recognizing the cardiac vulnerable period. The electric utility companies and the telephone companies were vitally interested in the likelihood of accidental electric shock causing ventricular fibrillation. This concern led to a classic paper by Ferris and King where they recognized that shocks that occurred during the T wave of the electrocardiogram were more likely to cause ventricular fibrillation that shocks timed to occur during other phases of the electrocardiogram. The T wave is caused by the passage of the wave of repolarization, and corresponds to the unstable state described above, when the geometic distribution of refractoriness is ideal for supporting unidirectional propagation.
At Duke, we were very concerned about accidental electric shock and inducing ventricular fibrillation. We were aware of the vulnerable period but to make measurements in animals and humans with precise timing was not possible. Thus, we used 2 second bursts of 60 Hz current to measure the threshold of ventricular fibrillation. In man, the threshold of ventricular fibrillation with small electrodes was several hundred microamperes. (see reference below).
Andy Wallace was puzzled by this low threshold, when it was well known that the capture threshold for cardiac pacemakers was several milliamperes - i.e. 10x greater. Andy developed a set of really clever studies where he showed that the threshold of VF was decreased following a PVC - and in fact, for a train of electrically induced PVCs the threshold of VF approached that of our experiments. (see reference below). Looking back on these studies, I suspect that with each successive PVC, the conduction velocity was slowed, thus increasing the period of vulnerability and lowering the threshold of VF.
- Garrey, W.E. 1914. The nature of fibrillary contraction of the heart. Its relation to tissue mass and form. Amer. J. Physiol. 33:397-414.
- Hooker, D.R., Kouwenhoven, W.B. and Langworthy, O.R. The effect of alternating current on the heart. Amer. J. Physiol. 103:444- ,1933.
- Ferris, L.P., King, B.G., Spence, P.W. and WIlliams, H.B. Effect of electric shock on the heart. Electrical Engineering 55:498-515, 1936.
- Wiggers, C.F. and Wegria, R. 1939. Ventricular fibrillation due to single localized induction in condenser shock supplied during the vulnerable phase of ventricular systole. Am. J. Physiol 128:500-505.
- Sugimoto, T., Schaal, S.F. and Wallace, A.G. Factors determining vulnerability to ventricular fibrillation induced by 60-CPS alternating current. Circulation Res 221:601-608, 1967.
- Starmer, C.F. and Whalen, R.E. 1973. Current density and electrically induced ventricular fibrillation. Medical Instrumentation 7:158-161
- Yamanouchi, Y, Yuanna, C, Tchou, P.J. and Efimov, I.R. The mechanism of the vulnerable window: the role of virtual electrodes and shock polarity. Can. J. Physiol. Pharmacol 79:25-33, 2001.
- Igor Efimov's short history of fibrillation and defibrillation
Proarrhythmic Effects of "Antiarrhythmic" Drugs: The Guarded Receptor Model and its use to Identify Proarrhythmic Drug Effects
In addition to the understanding of the proarrhythmic nature of electric shock, drugs that alter membrane properties can also exhibit proarrhythmic properties. Early signs of problems with cardiac drugs began to appear in the literature during the early 1980s. During this time, we were developing a model of how drugs interacted with membrane ion channels - This was followed by a series of studies that demonstrated both theoretically as well as with numerical and invitro experiments, the proarrhythmic side of many "antiarrhythmic" drugs. The main idea was that Na channel blockade reduces excitablility. Reducing excitability has two secondary effects:
- the probability of spontaneous oscillatory (premature impulse formation) is reduced, an antiarrhythmic effect
- conduction velocity is slowed, which increased the duration of the vulnerable period, a proarrhythmic effect.
Experimental studies suggested that use-dependent ion channel blockade was more effective then simply reducing the Na channel conductance. The story of use-dependent and frequency-dependent blockade is often lost. The first observations that I am aware of were by Ted Johnson and his group. This was followed by West and Amory and then Peter Heistracher. Clay Armstrong was the first to suggest a simple model of ion channel blockade, in this case, TEA block of potassium channels in squid giant axon.
- Johnson, E.A. and McKinnon, M.G. 1957. The differential effect of quinidine and pyrilamine on the myocardial action potential at various rates of stimulation. J. Pharm. Exp. Ther 120:460-468.
- West, T.C. and Amory, D.W. 1960. Single fiber recording of the effects of quinidine at atrial and pacemaker sites in the isolated right atrium of the rabbit. J. Pharm. Exp. Ther. 130: 183-193. Early references to use-dependent ion channel blockade
- Heistracher, P. 1964. Elektrophysiologische untersuchungen uber den mechanismus der wirkung eines antifribillans auf de antiegssteilheit des aktionspotentials fon purkinje-fasrn. Pflugers Archiv 279:305-329.
- Armstrong, C.M. 1969. Inactivation of the potassium conductance and related phenomena caused by quaternary ammonium ion injection in squid axons. J. Gen Physiol. 54:553-575.
The clinical worlds was active describing the proarrhythmic effects of Class I antiarrhythmic drugs. From my perspective, all these clinical studies reflected a common denominator, that of reduced excitability and slowed conduction. Slowed conduction prolonged the period of vulnerability, as shown by Wiener and Rosenbleuth and so, there seemed to be a clear cut mechanistic link between use-dependent Na channel blockade and amplified proarrhythmia. Unfortunatly, this physical mechanism has never really caught the imagination of clinical investigators. Here are a few several useful references:
- Nathan, A.W., Hellestrand, K.J., Bexton, R.D., Banim, S.O., Spurrel, R.A.J. and Camm, A.J. 1984. Proarrhythmic effects of the new antiarrhythmic agent flecainide acetate. American Heart J. 107:222-228.
- Boehnert, M.T. and Lovejoy, F.H. 1985. Value of the QRS duration versus the serum drug level in predicting seizures and ventricular arrhythmia after an acute overdose of tricyclic antidepressants. N. Engl. J. Jed. 313:474-479.
- Whitcomb, D.C., Gilliam, F.R., Starmer, C.F. and Grant, A.O. 1989 Marked QRS complex abnormalities and sodium channel blockade by propoxyphene reversed with lidocaine. Journal of Clinical Investigation 84:1629-1636
- Herre, J.M., Titus, C., Oeff, M., Eldar, M., Franz, M.R., Griffin, J.C. and Scheinman, M.M. 1990. Inefficacy and proarrhythmic effects of flecainide and encainide for sustained ventricular tachycardia and ventricular fibrillation. Ann. Intern. Med. 113:671-676.
- Bauman, J.L., Graw, J.J., Winecoff, A.P. and Hariman, R.J. 1994. Cocaine-related sudden cardiac death: a hypothesis correlating basic science and clinical observations. J. Clin. Pharmacol 34:902-911.
- Krishnan, S.C. and Josephson, M.E. 1998. ST segment elevation induced by class IC antiarrhythmic agents: underlying electrophysiologic mechanisms and insights into drug-induced proarrhythmia. J. Cardiovasc. Electrophysiol 11:1167-1172.
- Weiner, A.L., Vieira, L., McKay, C.A. and Bayer, M.J. 2000. Ketamine abusers presenting to the emergency department: a case series. J. Emerg. Med. 18:447-451.
The "classic" paper on the "bad" side of antiarrhythmic drugs was published in the New England Journal of Medicine in 1989:
- The Cardiac Arrhythmia Suppression Trial (CAST) investogators. 1989. Preliminary report: effect of encainide and flecainide on mortality in a randomized trial of arrhythmia suppression after myocardial infarction. N. England. Journal of Med. 321:406-412.
Our studies starting in the early 80s, occurred in parallel with the clinical trials. Our goal was to develop a physical model of Na channel blockade and identify the role of reduced excitability and slowed propagation associated with use-dependent Na channel block in amplifying the period of vulnerability.
- Starmer, C.F., Grant, A.O. and Strauss, H.C. 1984. Mechanisms of use-dependent block of sodium channels in excitable membranes by local anesthetics. Biophysical J. 46:15-27.
- Starmer, C.F. and Grant, A.O. 1985. Phasic ion channel blockade: a kinetic model and method for parameter estimation. Molecular Pharmacology. 28:348-356.
- Starmer, C.F., Yeh, J.Z. and Tanguy, J. 1986. A quantitative description of QX222 blockade of sodium channels in squid giant axon. Biophysical J. 49:913-920.
- Starmer, C.F. 1988. Characterizing activity-dependent processes with a piecewise exponential model. Biometircs, 44:549-559.
- Whitcomb, D.C., Gilliam, F.R., Starmer, C.F. and Grant, A.O. Marked QRS complex abnormalities and sodium channel blockade by propoxyphene reversed with lidocaine. Journal of Clinical Investigation 84:1629-1636, 1989
- Colatsky, T.J., Follmer, C.H. and Starmer, C.F. 1990. Channel specificity in antiarrhythmic drug action: mechanism of potassium channel block and its role in suppressing and aggravating cardiac arrhythmias. Circulation. 82:2235-2242.
- Starmer, C.F., Lastra, A.A., Nesterenko, V.V. and Grant, A.O. Proarrhythmic response to sodium channel blockade: Theoretical model and numerical experiments. Circulation 84:1364-1377, 1991.
- Starmer, C.F., Biktashev, V.N., Romashko, D.N., Stepanov, M.R., Makarova, O.N. and Krinsky, V.I. 1993. Vulnerability in homogeneous excitable media: Analytical and numerical studies of unidirectional propagation, Biophysical Journal, 65:1775-1787.
- Starobin, J., Zilberter, Y.I. and Starmer, C.F. 1994. Vulnerability in one-dimensional excitable media. Physica D. 70:321-341.
- Starobin, J., Zilberter, Y.I., Rusnak, E.M. and Starmer, C.F. Wavelet formation in excitable cardiac tissue: The role of wavefront-obstacle interactions in initiating high frequency fibrillatory-like arrhythmias. Biophysical J. 70:581-594, 1996.
- Starmer, C.F. The cardiac vulnerable period and reentrant arrhythmias: Targets of anti- and proarrhythmic processes. Pace 20:445-454, 1997.
How Does a Simple Reentrant Wave Fractionate? A Model of Fibrillation? And, the Liminal Length of Rushton and Kolmogorov Revisited
The CAST studies cited above were comprised of patients that had survived a myocardial infarction (heart attack). Moreover, these patients were treated with drugs in sufficient dose to suppress >80% of premature or extra excitations. I realized that something quite interesting was happening in patients with structural heart disease and who were being treated with antiarrhythmic drugs. While we (myself, Krinsky, Romashko, Biktashev, Starobin) had been successful in characterizing the nature of the cardiac vulnerable period in a homogeneous medium, something was absent. Spach's work on the role of structural discontinuities, and the arrhythmic potential of strucutural discontinuities turned out to be the missing link. Madison Spach (Maddy) and I have run together for the past 15 years and during our noon, running seminars, we would always use the first first miles to enlighten the other of our recent insights and progress. It was during this 15 year seminar, that I slowly came to realize the importance of Maddy's work, and in particular the role of safety factor (originally described by Rushton in 1937) in determining whether a wave could be blocked.
Joseph Starobin, in our studies of models that led to high frequency arrhythmias, had used an obstacle to create a wave break and initiate spiral activity. While Joseph was excited about the resultant high frequency arrhythmias, I was fascinated by the outcome of the obstacle- wave collision. We found that there was a critical velocity, below which the wave separated from the obstacle boundary and above which, the wave maintained contact with the obstacle boundary. Joseph had developed a very clever approximation of the boundary layer adjacent to the wave front in our 1D Physica D paper
- Starobin, J., Zilberter, Y.I. and Starmer, C.F. 1994. Vulnerability in one-dimensional excitable media. Physica D. 70:321-341.
in order to estimate the conditions for unidirectional conduction associated with premature stimulation. As we looked carefully at the 2D results of wave-obstacle collisions, we immediately recognized that the same analysis could be used to approximate the conditions for wave-obtacle separation. Of course, we were concerned about the details of the wave-obstacle interaction and so considered what happened when the angle between the velocity vector and the obstacle boundary was altered - and the most obvious question, what happens when the angle is 180 degrees - i.e. a then strip, parallel to the wave velocity vector?
We found that one could approximate wave-obstacle interaction by considering the balance between diffusive fluxes away from the wave and the reactive flux available within the wavefront. Moreover, we found that when the thickness of the obstacle (oriented parallel to the wave velocity vector) was of the order of the wave front thickness, then the wave-obtacle separation conditions were the same as that associated with the transition from circular spiral tip motion to noncircular (meandering) spiral tip motion.
- Starobin, J., Zilberter, Y.I., Rusnak, E.M. and Starmer, C.F. Wavelet formation in excitable cardiac tissue: The role of wavefront-obstacle interactions in initiating high frequency fibrillatory-like arrhythmias. Biophysical J. 70:581-594, 1996.
- Starobin, J.M. and Starmer, C.F. Boundary-layer analysis of waves propagating in an excitable medium: Medium conditions for wave-front--obstacle separation. Phys. Rev. E 54:430-437, 1996.
- Starobin, J.M. and Starmer, C.F. A common mechanism links spiral wave meandering and wavefront-obstacle separation. Phys Rev. E 55:1193-1197, 1997.
- Starobin, J.M., Starmer, C.F. and Starobin, A.J. Boundary-layer analysis of a spiral wave core: Spiral core radius and conditions for the tip separation from the core boundary. Phys Rev E.56:R3757-R3760, 1997.
These papers complemented my earlier paper that demonstrated that K channel blockade, specifically reducing the the inward rectifier conductance which produced both a prolongation of the action potential duration as well as increased the net inward current accumulated within the wave front, increased the degree of meandering of a rotating spiral wave. We felt we had identified a generic mechanism for producing meandering within cardiac preparations, and were able to demonstrate the effect in both Fitzhugh-Nagumo and Beeler-Reuter models. Our results showed us that understanding the nature of front formation of a propagating wave was essential for understanding the nature of different types of reentrant cardiac arrhythmias as well as to developing rational control strategies.
Our current challenge is to improve our understanding of wavefront formation and more specifically, to understand the nature of our approximation of the reactive and diffusive fluxes within the boundary layer. Our primary goal is to develop control strategies by manipulating conditions at the spiral tip that alter where the tip can extend (propagate) and where it fail to propagate. Here Tassos Bountis (Dept of Mathematics, University of Patras) and I have worked out the analytical solution for a stationary pulse in 1D medium (of the form
where A, a, b, c, d are determined by the properties of the excitable medium (here we used the FitzHugh-Nagumo model with a cubic reaction process: dU/dt = U(1-U*U) - W + d2U/dx2.
- Bountis, T., Bezerianos, T. and Starmer, C.F. Wave front formation in an excitable medium by perturbation of solitary pulse solutions. in Proceedings of the 4th School "Lets Face Chaos through Nonlinear Dynamics" Maribor, Slovenia, 1999, Ed. by M. Robnik. Prog. Theor. Phys. Suppl. 139: 12-33, 2000.
Observing Reentrant Activation with Optical Methods
"While all this theoretical work has been going on, the experimentalists in the cardiac world have not been quiet. Pepe Jalife's lab first demonstrated spiral like patterns during reentry initiated in optical studies of slices of ventricular myocardium from sheep. As related by Dante Chialvo: " Around 1989, the first spirals in Syracuse were obtained and mapped by myself (Chialvo) and Jorge Davidenko borrowing Paul Kent (grad student in physiology doing olefaction in the salamander) flourescence set-up."
"How the project started is another (funny story). Davidenko, just arrived from Argentina and was experimenting with some Na-channel poisson Jalife told him to try in slices of sheep ventricle, because of disagreement if the chaotic (in the vernacular sense) activity was reentry or triggered activity."
"At the same time, I just finished reading Winfree's book (stolen from Michaels' desk!) and was eager to experiment in the slices with the s1-s2 cross-field stimulation. Thus I designed and built for Jorge's tissue chamber to include wires running orthogonal to each other (as depicted in the figure of the paper). It took less than an hour to fiddle with timing and amplitudes of pulses to get very reproducible self-sustained activity in the slices. There was a real excitement, the theory worked perfectly. The next step was to convince Kent to use his set-up and remove his salamander olefactory bulb to let us play with the ventricular slices. The rest was a lot of "data massage" and Don Michaels' numerical work to make nice pictures."
These initial studies were followed by some very elegant and beautiful demonstrantions from Peng-Sheng Chen's lab and Igor Efimov's lab.
- Davidenko, Kent, Michaels, Chialvo and Jalife. Sustained vortex-like waves in normal isolated ventricular muscle. Proc. Natl. Acad Sci, USA 355:349-351, 1990.
- Lee, J.J., Kamjoo, K., Hough, D., Hwang, C., Fan, W., Fishbein, M.C., Bonometti, C., Ikeda, T., Karagueuzian, H.S. and Chen P.S. Reentrant wavee fronts in Wiggers' stage II ventricular fibrillation: characteristics and mechanisms of termination and spontaneous regeneration. Circ. Res. 78: 660-675, 1996.
- Pertsov, A.M., Davidenko, F.M., Salomonsz, R., Baxter, W.T. and Jalife, J. Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circulation Research 72:631-650, 1993.
- Ikeda, T., Uchida, T., Hough, D., Lee, J.J., Fishbein, M.C., Mandel, W.J., Chen, P-S and Karagueuzian, H.S. Mechanism of spontaneous termination of functional reentry in isolated canine right atrium. Evidence for the presence of an excitable but nonexcited core. Circulation 94:1962-1973, 1996.
New Insights into Vulnerability and Defibrillation:
Fibrillation is complex, as we have outlined above. Fibrillation is initiated by creating a wavelet or, what I call, a discontinuous wave. This wave curls at its ends and becomes a spiral. The path of the spiral is determined by the energy in the front and the state of the excitable medium. Now the big unanswered question is how to stop it.
Defibrillation is, in my mind, much more complex that fibrillation. I can visualize vulnerability, wave fragmentation etc. Defibrillation on the otherhand is basically pressing the reset button. But what is the resetting process. Krinsky has been chasing this question as long as I have known him. Ray Ideker and Igor Efimov have joined the chase. And at the same time, the theoreticians have not been sitting on their hands.
The basic principles of defibrillation were articulated (thanks to Igor Efimov) by Gurvich in 1975 (see reference below). In addition, the theoretical world has been struggling with ways to characterize wave motion when there were significant extracellular currents - developing the bidomain methods. Here are some useful references:
- Gurvich, N.L. 1975. Basic Principles of Defibrillation (Ocnovnie printsipi defibrillyatsi cerdtsa) (in Russian)
- Muler AL, Markin VS. [Electrical properties of anisotropic neuromuscular syncytia. I. Distribution of the electrotonic potential]. Biofizika. 1977; 22:307-312.
- Muler AL, Markin VS. [Electrical properties of anisotropic neuromuscular syncytia. II. Distribution of a flat front of excitation]. Biofizika. 1977; 22:518-522.
- Muler AL, Markin VS. [Electrical properties of anisotropic neuromuscular syncytia. III. Steady state of the front of excitation]. Biofizika. 1977; 22:671-675.
 Igor Efimov
(also a product of Krinsky's lab, and I met during my 1992 work on
vulnerability with Krinsky in Pushchino shown here with his daughter, Masha)
showed with really elegant studies that bilayer properties are
essential for exploring responses to cardiac excitation.
What he has observed is that the
dog-bone like pattern associated with transcellular stimulation results
in alternating regions of hyper- and depolarized tissue and creates
the possibility for either defibrillation or maintaining fibrillatory
processes. Up until Igor's observations, there was great uncertainty as
to why biphasic defibrillation waveforms were more successful than
monophasic waveforms. These were extremely elegant studies - and an uphill
challenge to the established ideas originating from the mono-domain
world.
Igor Efimov
(also a product of Krinsky's lab, and I met during my 1992 work on
vulnerability with Krinsky in Pushchino shown here with his daughter, Masha)
showed with really elegant studies that bilayer properties are
essential for exploring responses to cardiac excitation.
What he has observed is that the
dog-bone like pattern associated with transcellular stimulation results
in alternating regions of hyper- and depolarized tissue and creates
the possibility for either defibrillation or maintaining fibrillatory
processes. Up until Igor's observations, there was great uncertainty as
to why biphasic defibrillation waveforms were more successful than
monophasic waveforms. These were extremely elegant studies - and an uphill
challenge to the established ideas originating from the mono-domain
world.
Art Winfree for years overlooked these issues. Following a number of discussions with Igor, Art accepted a new way of looking at the role of the defibrillation waveform. Art revised his website to reflect his new understanding:
"What is the ultimately simplest indispensable foundation principle underlying Efimov's surprising discovery of "Virtual Electrode Induced Phase Singularities" ? Until Nov 98 I thought it was the inequality of electrical anisotropies in cardiac muscle. This enables a single shock from a single point-like electrode to induce a pattern of positive and negative polarizations in the neighborhood, from which rotor pairs arise even in the absence of any pre-existing gradient of refractoriness. This is so utterly different from all schemes familiar to me for creating phase singularities that I was intrigued to find the elemental difference from my schemes. It turned out to be the patterned stimulus imprint. Even in uniform FitzHugh-Nagumo model excitable media without any anisotropy, let alone unequal dual anisotropies, rotor pairs can arise if a suitably patterned stimulus is imposed on uniformly quiescent medium, much to my surprise... "
- Efimov, I.R., Cheng, Y., VanWagoner, D.R., Mazgalev, Todor and Tchou, P.J. Virtual Electrode-Induced Phase Singularity: A basic mechanism of debifrillation failure. Circ Res 82:918-925, 1998
- Cheng, Y., Mowrey, K.A., van Wagoner, D.R. Tchou, P.J. and Efimov, I.R. Virtual electrode-induced reexcitation: A mechanism of defibrillation Circ. Res. 85:1056-1066, 1999.
- Lindbolm, A.E., Roth, B.J. and Trayanova, N.A. Role of virtual electrodes in arrhythmogenesis: Pinwhell experiment revisited. J. Cardiovasc. Electrophysiol. 11:274-285, 2000.
Something about my confusion with phase singularities
Due to the charge requirments associated with extending the wave into excitable regions, the ends of the wave fragment will face a higher load for extension, (exciting media in front as well as to the side) than wave segments between the ends (which only must excite the media in front) and thus will propagate more slowly than segments of the front between the ends. The curvature of the front at the ends must surely be determined by the amount of charge available in the ends of the wave fragment - with greater charge (secondary to higher gNA) resulting in a larger current source thereby creating higher curvature of the ends while less source charge (secondary to reduce gNa perhaps associated with use-dependent Na channel blockade) will require longer to bring adjoining regions to threshold thus slowing the velocity and reducing the front curvature. As the ends of a wavelet develop there will appear a point where the wave front becomes the wave back. This is clearly a singularity, but it is the result of evolution of the front and the wave back from its initial fragment?
I believe the concept of phase singularity has acquired a confusion factor and sometimes is used to refer to the spiral core. Theoertical analyses
- Zykov, V.S. Simulation of wave processes in excitable media (Nauka, Moscow 1984) [English translation: Manchester Univ. Press, Manchester 1987).
- Keener, J.P. and Tyson, J.J. Singular perturbation theory of traveling waves in excitable media. Physica D 32: 327-361, 1988.
- Meron, Ehud. The role of curvature and wavefront interactions in spiral wave dynamics. Physica D. 37:98-106, 1991.
The relationship between curvature, K, and velocity,V(K) = V0 + b*K is based on the singular approximation.
- Zykov. V.S. Kinematics of the steady circulation in an excitable medium. Biofizika 26:319-322, 1980.
It seems to me useful restrict the use of the curvature-velocity association and drop back into the front itself and ask, ok, what are the determinants of front movement, what makes the front curve and how fast is the front able to expand into adjoining regions (velocity)? Will these questions lead to new insights into the stabile and unstable regions of spiral propagation? Consider cardiac preparations. For cardiac preparations, it is the inward Na current that creates excess + charge in the front region (where the Na channels open). This excess charge then has to go somewhere (down the intracellular corridor and to adjoining cells via gap junctions)in order to restore charge equilibrium. The spatial gradient of membrane potential probably dominates this motion over ionic diffusion gradients (my assumption). So excess charge must flow into adjoining antegrade resting regions since they provide the largest gradient in membrane potential. There is very little potential gradient in the retrograde direction (along the action potential plateau), thus there will be very little + current flow into adjoining repolarizing cells. If one accepts this, then the spiral core dimensions and the transition to menandering are probably dominated by the excess charge available within the front (source) and the excitability of adjoining cells (sink). Consequently, drugs that reduce front charge (Na blockade, gap junction decouplers) will appear to be stabilizers of spiral motion, whereas drugs that increase front charge (such as block of the inward rectifier or mutant Na channels with delayed inactivation) will appear to destabilize front motion. This provides a convenient explanation for polymorphic arrhythmias in LQT and the transition to monomorphic arrhythmias associated with Na channel blockade) see:
- Starmer, C.F. Reddy, M.R., Namasivayam, A. and Singh, M. Potassium channel blockade amplifies cardiac instability: numerical studies of torsades de pointes. Ind. J. Physiol. Pharm 38:259-266, 1994.
- Horowitz, L.N., Greenspan, A.M., Spielman, S.R. and Josephson, M.E. Torsades de pointes: electrophysiologic studies in patients without transient pharmacologic or metabolic abnormalities. Circulation 63:1120-1127, 1981. (Patients with inducible polymorphic VP could not be induced after administering procainamide, a Na channel blocker. Our interpretation is that the Na block reduced the available excess charge in with front such that both conduction velocity was reduced and the ends of a wave fragment were no longer able to make high curvature leading to meandering.)
Revisiting old problems with new insights
A recent example is from Lars Endresen who has explored the physics of the membrane potential: A theory for the membrane potential for cells We will continue to update this reading list with other interesting "stuff" - from both the biological and the computer science perspective.
 This essay is my view of the links between a number of different
areas of investigation in chemistry (BZ redox wave motion),
in mathematics (the Fitzhugh-Nagumo characterization of an excitable medium)
and cardiac electrophysiology - all leading to an understanding of how
cardiac arrhythmias are initiated and maintained. The majority of
these ideas were ignited in a course on Excitable Cell Physiology given
by
This essay is my view of the links between a number of different
areas of investigation in chemistry (BZ redox wave motion),
in mathematics (the Fitzhugh-Nagumo characterization of an excitable medium)
and cardiac electrophysiology - all leading to an understanding of how
cardiac arrhythmias are initiated and maintained. The majority of
these ideas were ignited in a course on Excitable Cell Physiology given
by
 Each of my mentors conveyed essential insights to me. John Moore and
Paul Horowitz revealed the beauty and simplicity in the physics
underlying complex
biological processes. Jim Grizzle always looked for common denominators
among similar problems
and used these common denominators to develop a simple approach to problem
solving that removed many complexities others found
necessary. Gene Stead showed me that new insights
depended as much on hearing what was not said as hearing what was said.
Joe Greenfield showed me the power of visualizing data, not
just looking at tables. Jim Wyngaarden revealed how one consolidates ideas
from others and synthesizes a new insight.
Valentin Krinsky revealed the power of identifying
generic properties of an excitable medium and the utility of minimally
complex models. Gus Grant was the most compulsive experimentalist I've
ever worked with. If Gus put his approval on the data - it was perfect.
Each of my mentors conveyed essential insights to me. John Moore and
Paul Horowitz revealed the beauty and simplicity in the physics
underlying complex
biological processes. Jim Grizzle always looked for common denominators
among similar problems
and used these common denominators to develop a simple approach to problem
solving that removed many complexities others found
necessary. Gene Stead showed me that new insights
depended as much on hearing what was not said as hearing what was said.
Joe Greenfield showed me the power of visualizing data, not
just looking at tables. Jim Wyngaarden revealed how one consolidates ideas
from others and synthesizes a new insight.
Valentin Krinsky revealed the power of identifying
generic properties of an excitable medium and the utility of minimally
complex models. Gus Grant was the most compulsive experimentalist I've
ever worked with. If Gus put his approval on the data - it was perfect.
 Just after the 2nd World War, Hodgkin and
Huxley visited Cole and learned of this breakthrough in instrumentation.
H and H then went back to England and successfully used the technique
to understand the ionic basis of action potentials in nerve.
Hodgkin and Huxley won the Nobel prize for their work on the excitable
properties of the squid (loligo - see right) giant nerve.
Unfortunately, Cole's contribution (as Wiener's contribution) is often
lost within today's electorphysiology community.
The most recent advance
in electrophysiology was the "patch clamp", where one can explore the
electrical properties of single membrane-spanning channel proteins (see left).
Just after the 2nd World War, Hodgkin and
Huxley visited Cole and learned of this breakthrough in instrumentation.
H and H then went back to England and successfully used the technique
to understand the ionic basis of action potentials in nerve.
Hodgkin and Huxley won the Nobel prize for their work on the excitable
properties of the squid (loligo - see right) giant nerve.
Unfortunately, Cole's contribution (as Wiener's contribution) is often
lost within today's electorphysiology community.
The most recent advance
in electrophysiology was the "patch clamp", where one can explore the
electrical properties of single membrane-spanning channel proteins (see left).
 This work of Neher and Sakmann was rewarded with another Nobel prize, but
the contribution of Fred Sigworth in developing good low noise
amplifiers, on which the technique is dependent has gone mostly
unrecognized.
This work of Neher and Sakmann was rewarded with another Nobel prize, but
the contribution of Fred Sigworth in developing good low noise
amplifiers, on which the technique is dependent has gone mostly
unrecognized.


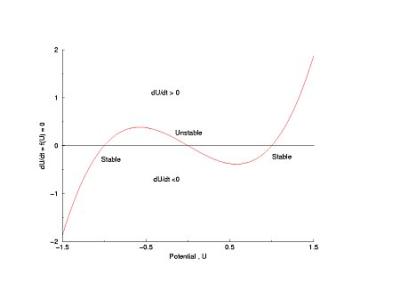
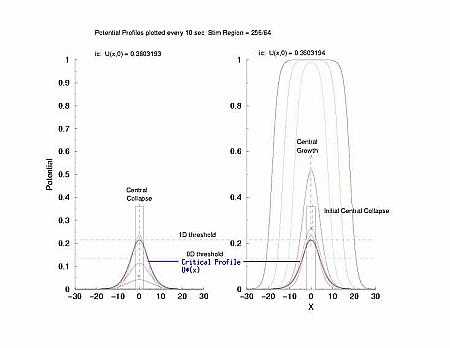
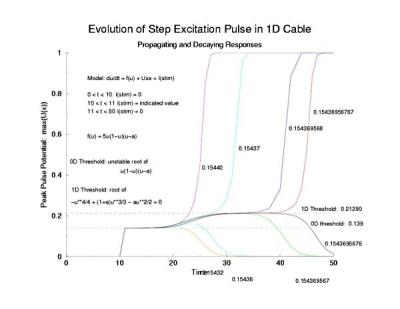
 In a uniformly excitable 2D medium, there is a
In a uniformly excitable 2D medium, there is a
 Note
also that has increasing the inhibitory current (less negative values)
further reduces the rest potential (the constant regions either side of the
critical nucleus.
Note
also that has increasing the inhibitory current (less negative values)
further reduces the rest potential (the constant regions either side of the
critical nucleus.