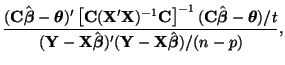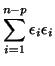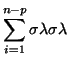Next: .
Up: Derivations For the Curious
Previous: .
Index
Click for printer friendely version of this HowTo
Proof of 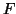 -Distribution
-Distribution
The goal here is to show that Equation 3.13.21, that is
has an 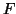 -distribution. We will do this by showing that the numerator
and the denominator are both
-distribution. We will do this by showing that the numerator
and the denominator are both 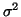 times chi-square variables
divided by their degrees of freedom.
times chi-square variables
divided by their degrees of freedom.
Since
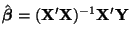 is a linear function of Y, and
is a linear function of Y, and
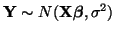 , a vector of
, a vector of  iid
random variables, it follows from
Equations 3.13.7 and 3.13.8 that
iid
random variables, it follows from
Equations 3.13.7 and 3.13.8 that
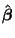 is a vector of
is a vector of 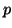 random variables with a
random variables with a
![$ N(\boldsymbol{\beta}, \sigma^2[{\bf X}'{\bf X}]^{-1})$](img1168.png) distribution. Thus, the transformation,
distribution. Thus, the transformation,
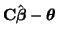 , results in
, results in  random variables (
random variables ( being the number of rows in C, the
number of tests):
being the number of rows in C, the
number of tests):
Under the hypothesis that
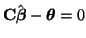 we have,
thus,
we have,
thus,
Since the sum of  squared iid
squared iid  variables results in a random
variable distributed by
variables results in a random
variable distributed by 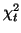 , it follows from
Equation D.7.1 that,
Thus, we have shown that the numerator in Equation 3.13.21 is
, it follows from
Equation D.7.1 that,
Thus, we have shown that the numerator in Equation 3.13.21 is
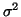 times a chi-square random variable divided by its degrees
of freedom.
times a chi-square random variable divided by its degrees
of freedom.
Showing the same thing for the denominator is a little more tricky as
it involves some obscure transformations and knowing a few properties
of quadratic forms. Instead of trying to explain the details about
quadratic forms that would be required for a full proof, we'll simply
go as far as we can with what we have and appeal to your sense of intuition.
Let
 ,
an approximation of the error vector,
,
an approximation of the error vector,
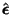 ,
thus,
,
thus,
and
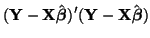 |
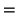 |
![$\displaystyle [({\bf I} - {\bf X}({\bf X}'{\bf X})^{-1}{\bf X}')\boldsymbol{\epsilon}]'
[({\bf I} - {\bf X}({\bf X}'{\bf X})^{-1}{\bf X}')\boldsymbol{\epsilon}]$](img1188.png) |
|
| |
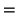 |
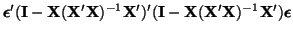 |
(D.7.2) |
| |
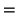 |
 |
(D.7.3) |
| |
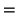 |
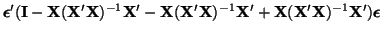 |
(D.7.4) |
| |
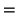 |
 |
(D.7.5) |
Equations D.7.2, D.7.3, D.7.4 and D.7.5
make it clear that
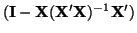 is idempotent, that is,
is idempotent, that is,
We can determine the rankD.1 of
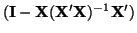 from its trace
(that is, the sum the elements on the diagonal) since it is idempotent and symmetric. Using a well known
property of traces, that is, tr
from its trace
(that is, the sum the elements on the diagonal) since it is idempotent and symmetric. Using a well known
property of traces, that is, tr tr
tr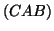 , and the fact
that X is an
, and the fact
that X is an
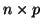 matrix, we have
matrix, we have
Since
 , it follows that
, it follows that
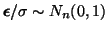 , thus we can imagine that
Equation D.7.5 is the sum of
, thus we can imagine that
Equation D.7.5 is the sum of 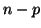 independent
normal random variables. Thus, if we let
independent
normal random variables. Thus, if we let
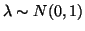 , then
, then
Showing that the numerator is independent from the denominator
also requires some obscure transformations and requires another result
from quadratic forms. Without proof, I will state that the following theorem.
Let Z is a vector of of normally distributed random
variables with a common variance and let
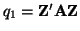 and
and
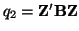 , where A and B are both
, where A and B are both
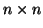 symmetric matrices.
symmetric matrices.  and
and 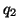 are independently
distributed if and only if
are independently
distributed if and only if
 .
.
Now, to show independence, under the hypothesis that C
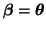 , can re-write the ends
of the numerator with
, can re-write the ends
of the numerator with
If we let
![$ {\bf A} = {\bf X}({\bf X}'{\bf X})^{-1}{\bf C}\left[ {\bf C}({\bf X}'{\bf X})^{-1}{\bf C} \right]^{-1}{\bf C}({\bf X}'{\bf X})^{-1}{\bf X}'$](img1221.png) , then we can rewrite the numerator of
Equation 3.13.21 as
, then we can rewrite the numerator of
Equation 3.13.21 as
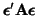 . If we let
. If we let
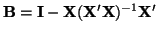 , then we can rewrite the
denominator to be
, then we can rewrite the
denominator to be
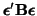 . Since
. Since
 , and thus, under the hypothesis, the numerator and
denominator are independent.
, and thus, under the hypothesis, the numerator and
denominator are independent.




Next: .
Up: Derivations For the Curious
Previous: .
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19