



Next: Hypothesis Testing
Up: Linear Models
Previous: Parameter Estimation: The Least
Index
Click for printer friendely version of this HowTo
If we assume that the elements in the noise vector,
 , are independent and normally distributed
3.15random variables with
, are independent and normally distributed
3.15random variables with
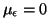 and
and
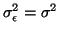 , (which is
not terribly unreasonable to do since noise can come from all kinds of
sources and once we add them all up, the central limit theorem kicks
into effect,) then we can determine if
, (which is
not terribly unreasonable to do since noise can come from all kinds of
sources and once we add them all up, the central limit theorem kicks
into effect,) then we can determine if
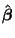 is
biased and what its variance is.
is
biased and what its variance is.
Before we start, however, we will note that the assumption that
 are independent and identically distributed
normal(0,
are independent and identically distributed
normal(0, 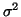 ) variables
implies that Y is also
normally distributed with mean
) variables
implies that Y is also
normally distributed with mean
 and
variance
and
variance 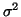 . This is because
. This is because
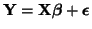 and
and
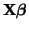 functions as
a location parameter.
functions as
a location parameter.
First, we will show that
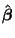 is unbiased.
is unbiased.
Now we will derive the variance of
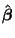 .
However, before we get into it, let me first point out that E
.
However, before we get into it, let me first point out that E
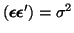 . This
can be easily shown using the facts that Var
. This
can be easily shown using the facts that Var
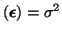 , E
, E
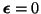 and the definition of variance. That is,
and the definition of variance. That is,
With that little bit of extra information in hand, we are now ready to
derive the variance of
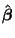 .
.
An alternative and shorter derivation of this same variance is as
follows:




Next: Hypothesis Testing
Up: Linear Models
Previous: Parameter Estimation: The Least
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19