|
|




Next: Using Matrix Algebra
Up: Methods for Solving ODEs
Previous: Separation of Variables
Index
Click for printer friendely version of this HowTo
Integrating Factors
Using integrating factors is a useful trick to use when you can not
separate the different variables or, if you are able to separate the
variables, the integration is too difficult. Here we will present an
example of how integrating factors are used and then give a general
formula for this method.
The simplest ODEs are linear with constant coefficients:
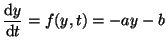 |
(2.10.8) |
where 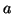 is a constant. You may have guessed that this is
similar to Equation 2.4.1, with a similar solution, the exponential
function (Equation 2.4.2). The only difference here
is that there is an added constant. Thus, just as you would expect,
the solution is exponential plus a constant.
Solving this equation, however, uses a trick, an integrating factor,
and in this case the integrating factor is is a constant. You may have guessed that this is
similar to Equation 2.4.1, with a similar solution, the exponential
function (Equation 2.4.2). The only difference here
is that there is an added constant. Thus, just as you would expect,
the solution is exponential plus a constant.
Solving this equation, however, uses a trick, an integrating factor,
and in this case the integrating factor is 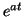 . The main idea is
to multiply the equation by a well chosen integrating factor that
makes the integration simple. The task of choosing a good integrating
factor can be boiled down to following a standard formula, so,
overall, finding the solution is not too hard. Thus, starting from
Equation 2.10.9, we can move everything to one side, . The main idea is
to multiply the equation by a well chosen integrating factor that
makes the integration simple. The task of choosing a good integrating
factor can be boiled down to following a standard formula, so,
overall, finding the solution is not too hard. Thus, starting from
Equation 2.10.9, we can move everything to one side,
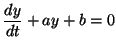 |
(2.10.9) |
and multiply through by 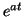 : :
We can now integrate both sides of the equation and get:
where 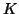 is an arbitrary integration constant that is determined by the initial conditions. is an arbitrary integration constant that is determined by the initial conditions.
To finally solve the equation we multiply through by  giving us: giving us:
or
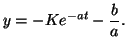 |
(2.10.10) |
To solve for 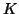 , we let , we let  and thus, and thus,
or
an the complete solution is written as
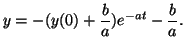 |
(2.10.11) |
To verify our solution is correct we can take the derivative of
Equation 2.10.12, plug it into Equation 2.10.10 and
make sure that everything cancels out. That is,
and from Equation 2.10.10
Plugging the results of Equations 2.10.13 and
2.10.14 into Equation 2.10.10, we have
which is exactly what it should reduce to.
In general, given the equation
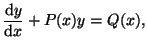 |
(2.10.14) |
the solution for 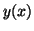 can be found with the formula can be found with the formula
![$\displaystyle y(x)= [\mu(x)]^{-1}\left( \int \mu(x)Q(x) \textrm{d}x + C\right),$](img408.png) |
(2.10.15) |
where 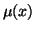 is the integrating factor and is the integrating factor and
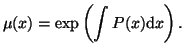 |
(2.10.16) |
no_titleno_title
In Example 2.4.0.1 we created the ODE:
which can easily be solved using this method. Following our recipe,
we have:
and after integrating both sides with respect to  , we have: , we have:
We can now solve for 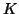 by setting by setting  : :
making our general solution:
or





Next: Using Matrix Algebra
Up: Methods for Solving ODEs
Previous: Separation of Variables
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |
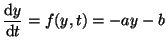
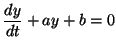
![$\displaystyle e^{at}\frac{\textrm{d}y}{\textrm{d}t} + aye^{at} + be^{at} = \frac{\textrm{d}}{\textrm{d}t} [y e^{at}] + be^{at} = 0.$](img390.png)
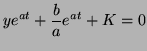
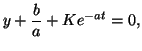
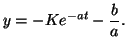
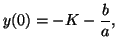
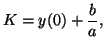
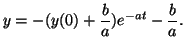
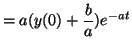
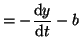
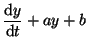
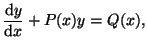
![$\displaystyle y(x)= [\mu(x)]^{-1}\left( \int \mu(x)Q(x) \textrm{d}x + C\right),$](img408.png)
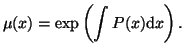

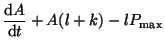
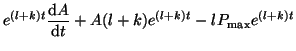
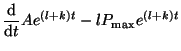
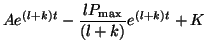
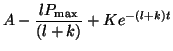
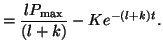
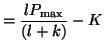
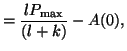
![$\displaystyle A(t) = \frac{lP_{\textrm{max}}}{(l+k)} - \left[\frac{lP_{\textrm{max}}}{(l+k)} - A(0)\right]e^{-(l+k)t},$](img423.png)
![$\displaystyle A(t) = \frac{P_{\textrm{max}}}{(1+\frac{k}{l})} - \left[\frac{P_{\textrm{max}}}{(1+\frac{k}{l})} - A(0)\right]e^{-(l+k)t}.$](img129.png)