



Next: Integrating Factors
Up: Methods for Solving ODEs
Previous: Graphical Solutions: Phase Plane
Index
Click for printer friendely version of this HowTo
How do we solve Equation 2.4.1? That is, how do we
determine what Equation 2.4.1 is the derivative of?
First, we note that we can separate the two variables, 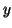 and
and  , by
multiplication. That is,
, by
multiplication. That is,
Integrating both sides produces
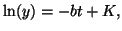 |
(2.10.4) |
where 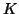 is the combination of the two integration constants. Using
each side as an exponent, we have
is the combination of the two integration constants. Using
each side as an exponent, we have
where 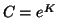 .
.
This method can be used to solve both linear as well as nonlinear
ordinary differential equations. Example 2.10.2.1 gives
an example of a solution to a quadratic nonlinear ODE and
Appendix D.2 shows how to use separation of
variables to solve a cubic nonlinear ODE.
Quadratic ODEno_title
We will begin with a quadratic ODE that is often used to model
population growth (birth and immigration) and decay (death and emigration).
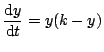 |
(2.10.5) |
Equation 2.10.5 can be solved using the method of
seperation of variables. We begin by separating 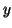 from
from  by
multiplcation. That is,
by
multiplcation. That is,
The integral on the right-hand side can be easily solved once it is
broken down into simpler components. This can be done using the
method of partial fraction decomposition. That is,
and
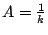 and
and
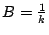 , thus,
, thus,
Substituting Equation 2.10.7 for the fraction in on the
left side of Equation 2.10.6 gives us the following:





Next: Integrating Factors
Up: Methods for Solving ODEs
Previous: Graphical Solutions: Phase Plane
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19