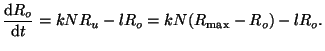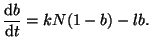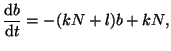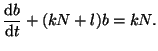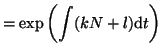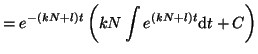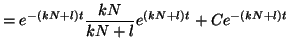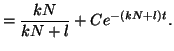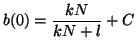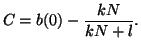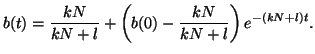|
|




Next: Microscopic/Probabilistic Behavior
Up: Examples of Models
Previous: Examples of Models
Index
Click for printer friendely version of this HowTo
Drug-Receptor Model Ino_title
Let's now look at a few examples of systems that lead to first order
differential equations. Consider the process of a neurotransmitter
binding to a receptor. Let 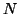 be the concentration of the neurotransmitter,
and be the concentration of the neurotransmitter,
and 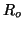 be the number of occupied receptors where be the number of occupied receptors where
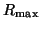 is the
total number of
receptors. The number of unoccupied receptors, is the
total number of
receptors. The number of unoccupied receptors, 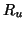 , is
thus , is
thus
 .
Thus, the reaction between neurotransmitter, unbound receptors and
bound receptors can be encapsulated with the formula, .
Thus, the reaction between neurotransmitter, unbound receptors and
bound receptors can be encapsulated with the formula,
where  is the proportionality constant for binding and is the proportionality constant for binding and 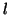 is the
proportionality constant for unbinding.
The rate of change of occupied receptors is thus, is the
proportionality constant for unbinding.
The rate of change of occupied receptors is thus,
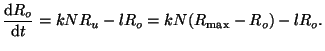 |
(2.8.1) |
If we convert Equation 2.8.1 to represent the change in the fraction
of bound receptors by dividing by
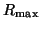 , and rearrange the terms a
little bit, then we can solve it by using what is called an integration factor.2.3That is, if we let , and rearrange the terms a
little bit, then we can solve it by using what is called an integration factor.2.3That is, if we let
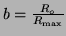 , we can rewrite
Equation 2.8.1 as , we can rewrite
Equation 2.8.1 as
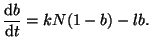 |
(2.8.2) |
Rearranging the terms gives us:
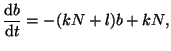 |
(2.8.3) |
or
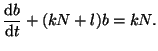 |
(2.8.4) |
With Equation 2.8.4 in the exact same form as
Equation 2.10.15, the form required for our general
solution, we can easily solve for 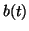 . First, we will determine
the integrating factor. That is, from Equations 2.8.4
and 2.10.17 . First, we will determine
the integrating factor. That is, from Equations 2.8.4
and 2.10.17
We can now plug the integrating factor, along with bits from
Equation 2.8.4 into Equation 2.10.16 and solve
for 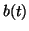 . Thus, . Thus,
Since we know that at time  that some fraction of receptors are
occupied, that some fraction of receptors are
occupied,  , we can solve for , we can solve for 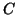 . That is, . That is,
and simple rearrangement gives us,
Thus, our general solution for 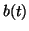 is is
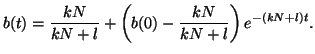 |
(2.8.7) |

Phase Plane Analysisno_title
If we return to Equation 2.8.3, we can determine the
asymptotic behavior of the solution without having to solve for it.2.4First, we will determine any points where the system is at
equilibrium. That is, determine where the derivative is zero.
Thus, when
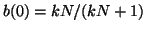 , for all , for all  , we are at an equilibrium and will not
move from it. When , we are at an equilibrium and will not
move from it. When
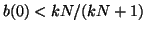 , then the slope for all , then the slope for all  is positive
(to see this, try plugging in is positive
(to see this, try plugging in
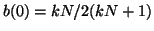 ), and thus, as ), and thus, as
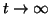 , , 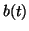 approaches approaches
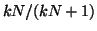 from below. If from below. If
 , then the slope for all , then the slope for all  will be negative and as will be negative and as
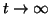 , , 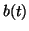 approaches the equilibrium from above. approaches the equilibrium from above.
Note that  when when 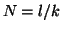 . This
is called the equilibrium dissociation constant and is the concentration of
drug where the fraction of bound receptors is 1/2. Thus, from the kinetics of
binding and unbinding, you can directly get a feel for the concentration
of drug required to have half the receptors occupied. . This
is called the equilibrium dissociation constant and is the concentration of
drug where the fraction of bound receptors is 1/2. Thus, from the kinetics of
binding and unbinding, you can directly get a feel for the concentration
of drug required to have half the receptors occupied.





Next: Microscopic/Probabilistic Behavior
Up: Examples of Models
Previous: Examples of Models
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |