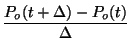Next: A Single Cell
Up: Examples of Models
Previous: Macroscopic/Deterministic Behavior
Index
Click for printer friendely version of this HowTo
Drug-Receptor Model IIno_title
Example 2.8.1.1 is probably
the most useful derivation in biological models. It is also simple
with only a few assumptions. If we look at the system more closely we see that
binding comes from molecules colliding with receptors and only every once in a while
is the collision sufficiently strong that an ``event'' takes place,
producing a complex of ``molecule bound to a receptor.''
The collisions are due to thermal motion and, up to a certain point,
the hotter the solution the more vigorous the collisions and the more
binding events. However, beyond that point, the
complex can also vibrate and fall apart. Thus, at thermal
equilibrium, both binding and unbinding events are constantly happening.
In Example 2.8.1.1 we were assuming that the
probability of a binding event or
an unbinding event is constant in time. In this example we will take
into account the microscopic view of binding and unbinding and
demonstrate that this this is a pretty solid assumption to make.
The probability that a receptor is occupied at time  is
is 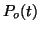 and
the probability that a receptor is unoccupied at time
and
the probability that a receptor is unoccupied at time  is
is 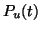 .
We also know that
.
We also know that
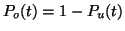 . The probability that an unoccupied
receptor will become occupied depends on the collision rate which in turn depends
on the concentration of hormones, neurotransmitters or whatever
molecule is involved in the reaction.
We will denote the concentration of the molecule as,
. The probability that an unoccupied
receptor will become occupied depends on the collision rate which in turn depends
on the concentration of hormones, neurotransmitters or whatever
molecule is involved in the reaction.
We will denote the concentration of the molecule as,
 . The probability that an unoccupied site at time
. The probability that an unoccupied site at time  will become occupied
during the next increment of time,
will become occupied
during the next increment of time,  is
is
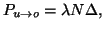 |
(2.8.8) |
where 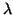 is the proportionality constant for the binding
rate per molecule of drug.
is the proportionality constant for the binding
rate per molecule of drug.
For a receptor is bound, there are two possibilities for its state
after 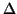 . It can either become unoccupied or remain occupied.
The probability that an occupied
receptor will become unoccupied during the time interval,
. It can either become unoccupied or remain occupied.
The probability that an occupied
receptor will become unoccupied during the time interval, 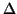 is
a fixed rate,
is
a fixed rate,
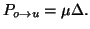 |
(2.8.9) |
The probability of
an occupied site remaining occupied during 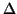 is
simply
is
simply
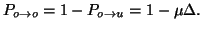 |
(2.8.10) |
To determine the probability that a site will be
occupied at time
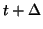 we need to consider two
possibilities. Either the site was empty at time
we need to consider two
possibilities. Either the site was empty at time  and became
occupied during
and became
occupied during 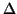 ,
or the site was occupied at time
,
or the site was occupied at time  and it did not become unoccupied during
the interval
and it did not become unoccupied during
the interval 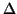 . Thus,
. Thus,
We can now rearrange terms in Equation 2.8.11 and make a difference equation,
If we now
let 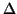 go to zero, we will end up with a differential equation for
the probability that a receptor site will become occupied:
go to zero, we will end up with a differential equation for
the probability that a receptor site will become occupied:
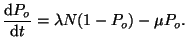 |
(2.8.13) |
If we compare Equation 2.8.13 to Equation
2.8.2 we notice a striking similarity. Notice that
where 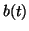 is the fraction of bound receptors at time
is the fraction of bound receptors at time  .
Also, both
.
Also, both 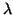 and
and 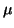 map to the
constants used in Equation 2.8.2. Thus, once we take
away the assumption that there is a constant event probability over
time, we end up with the same general equation.
map to the
constants used in Equation 2.8.2. Thus, once we take
away the assumption that there is a constant event probability over
time, we end up with the same general equation.





Next: A Single Cell
Up: Examples of Models
Previous: Macroscopic/Deterministic Behavior
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19