



Next: .
Up: Derivations For the Curious
Previous: Vector and Matrix Calculus
Index
Click for printer friendely version of this HowTo
If we let x an
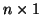 vector and let A be defined in
a similar fashion to A in Example D.3, only now
we require A to be an
vector and let A be defined in
a similar fashion to A in Example D.3, only now
we require A to be an
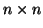 matrix, then
matrix, then
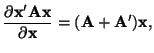 |
(D.4.1) |
and if A is symmetric, that is
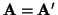 , then
, then
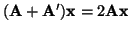 .
.
Once again, to understand how these results are derived we will simply
multiply out the matrices and then apply the definition of vector
differentiation (Equation 3.12.1). Thus,




Next: .
Up: Derivations For the Curious
Previous: Vector and Matrix Calculus
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19