Click for printer friendely version of this HowTo Vector and Matrix Calculus Let x be an $n \times 1$ vector and let A be an $m \times n$ matrix of elements that are not functions of x. Then $$\frac{\partial \bf Ax}{\partial \mathbf{x}} = {\bf A}'.$$ (D.3.1) To see this, we'll just multiply out Ax and then apply the definition of vector differentiation (Equation 3.12.1). Thus $$\frac{\partial \bf Ax}{\partial \mathbf{x}} = \frac{\partial... ...1} + a_{m, 2}x_{2} + \cdots + a_{m,n}x_{n} \end{array}\right],$$ and, in order to keep our matrix from getting too big for the page, let $$a_{1,1}x_{1} + a_{1, 2}x_{2} + \cdots + a_{1,n}x_{n} = {\bf a}_{1}{\bf x}$$ $$a_{2,1}x_{1} + a_{2, 2}x_{2} + \cdots + a_{2,n}x_{n} = {\bf a}_{2}{\bf x}$$ $$\vdots \vdots$$ $$a_{m,1}x_{1} + a_{m, 2}x_{2} + \cdots + a_{m,n}x_{n} = {\bf a}_{m}{\bf x}.$$ Thus, $$\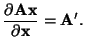frac{\partial}{\partial \mathbf{x}} \left[ \begin{array}{c} ... ...c{\partial}{\partial x_n} {\bf a}_{m}{\bf x} \end{array}\right]$$ $$=\left[ \begin{array}{cccc} a_{1,1}&a_{2,1}&\cdots&a_{m,1} ... ...\ a_{1,n}&a_{2,n}&\cdots&a_{m,n} \end{array}\right] = {\bf A}'$$ Click for printer friendely version of this HowTo

>