Click for printer friendely version of this HowTo Matrix Calculus Basically derivatives and integrals of matrices parallel derivatives and integrals of ordinary functions. The easiest way to figure out what the derivative or integral will be is to expand the matrix and then take an element by element derivative or integral. 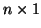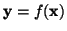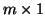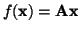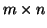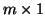If we let x be an $n \times 1$ vector and let ${\bf y} = f({\bf x})$, where y is an $m \times 1$ vector (for example, if $f({\bf x}) = {\bf Ax}$, where A is an $m \times n$ matrix, then y will be an $m \times 1$ vector), then $$\frac{\partial {\bf y}}{\partial \mathbf{x}} = \left [ \begin{arr... 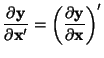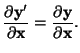...{\partial x_n}&\cdots&\frac{\partial y_m}{\partial x_n} \end{array} \right ].$$ (3.12.1) We will also include the following to our definition: $$\frac{\partial {\bf y}}{\partial {\bf x}'} = \left( \frac{\partial {\bf y}}{\partial {\bf x}} \right)'$$ (3.12.2) and $$\frac{\partial {\bf y}'}{\partial {\bf x}} = \frac{\partial {\bf y}}{\partial {\bf x}}.$$ (3.12.3) Now we'll list two very useful results.3.8 If x is an 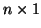$n \times 1$ vector and A is an 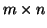$m \times n$ matrix of elements that are not functions of x, then 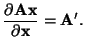$$\frac{\partial \mathbf{Ax}}{\partial \mathbf{x}} = \mathbf{A}'.$$ (3.12.4) If A is an 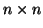$n \times n$ matrix of elements that are not functions of x, then 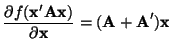$$\frac{\partial f(\mathbf{x'Ax})}{\partial \mathbf{x}} = {\bf (A + A}'){\bf x}$$ (3.12.5) and if A is symmetric, that is 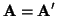${\bf A = A}'$, then $${\bf (A + A}'){\bf x} = 2{\bf Ax}.$$ Click for printer friendely version of this HowTo

>