


Next: Matrix Calculus
Up: Solving Constrained Optimization Problems
Previous: Solving Constrained Optimization Problems
Index
Click for printer friendely version of this HowTo
Figure:
A 3-D graph of two surfaces intersecting
![\includegraphics[width=3in]{graph3d}](img650.png) |
It is often the case that you have some function, for
example 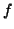 , and you want to find its extreme values (maximum
and or minimum). If
, and you want to find its extreme values (maximum
and or minimum). If 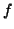 is a function of a single variable,
is a function of a single variable, 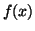 ,
then all that's needed is to take its derivative and check where it
equals zero. If we then went a little further and wanted the maximum
and minimum values of
,
then all that's needed is to take its derivative and check where it
equals zero. If we then went a little further and wanted the maximum
and minimum values of 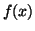 when
when 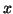 also falls on a specific line
(or is otherwise constrained by some other function
also falls on a specific line
(or is otherwise constrained by some other function 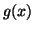 ),
then all we would need to do is find out where (and if) the two
lines intersected and check to see which values for
),
then all we would need to do is find out where (and if) the two
lines intersected and check to see which values for 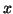 give us
the largest and smallest values from
give us
the largest and smallest values from 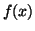 .
.
When functions of multiple variables are involved and we are still
trying to find constrained maximums and minimums, we do a similar
thing. In this case, instead of picturing lines intersecting, we can
imagine surfaces intersecting (see Figure 3.11.1). Regardless
of how we visualize the problem, there are two primary strategies for
solving this sort of problem. The first one, algebraic substitution,
works well when
there are only two variables involved (otherwise you run into the
problem of having more variables to solve for than you have
equations). In this case you simply use
the constraint equation to
solve for one variable in terms of another, substitute this solution
into the equation you wish to find the maximum/minimum of and then
take the derivative to solve for
the extreme points. The second method, Lagrange multipliers, (the
one we'll be covering
here), is a little more fancy, but works well when there are more than
two variables involved.3.63.7
To find the extreme values of
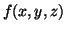 subject to the
constraint
subject to the
constraint
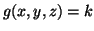 :
:
- Find all values of
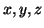 and
and 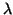 such that
such that
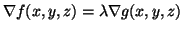 |
(3.11.1) |
and
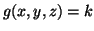
- Evaluate
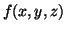 at all points,
at all points, 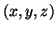 , that result
from the previous step.
, that result
from the previous step.
no_titleno_title
In this example we will use equations with only two variables and
demonstrate how both algebraic substitution and Lagrange multipliers
result in identical solutions.
Let's find the extreme values of
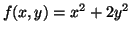 |
(3.11.2) |
that are also on the circle
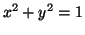 |
(3.11.3) |
(thus, in this case,
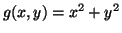 ).
).
Using Algebraic Substitution: Using the
constraint equation,
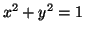 , we'll solve for
, we'll solve for 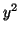 by moving
by moving
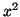 to the other side. Thus,
to the other side. Thus,
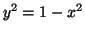 . We can then substitute
. We can then substitute
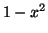 for
for 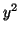 into
into
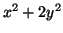 (Equation 3.11.2), giving us
(Equation 3.11.2), giving us
We can now take the derivative of Equation 3.11.4 and solve
for the extreme points. That is,
Combining Equation 3.11.5 with Equation 3.11.3, we
can determine that when 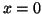 ,
, 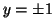 .
.
Now we must do the same thing only this time, we must use
Equation 3.11.3 to solve for 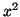 . That is, from
Equation 3.11.3,
. That is, from
Equation 3.11.3,
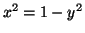 . Substituting this into
Equation 3.11.2, we then follow the same steps as before
to determine that when
. Substituting this into
Equation 3.11.2, we then follow the same steps as before
to determine that when 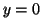 ,
, 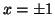 . We can then plug these
points into Equation 3.11.2 to find that Thus
. We can then plug these
points into Equation 3.11.2 to find that Thus
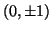 are both maximums and
are both maximums and
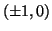 are both minimums.
are both minimums.
Using Lagrange Multipliers: To use the Lagrange multiplier method, we'll first set up the system of
equations defined by
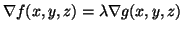 :
:
From Equation 3.11.6 we can determine that either 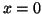 or
or
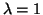 . If
. If 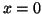 , the constraint equation,
(Equation 3.11.3), forces
, the constraint equation,
(Equation 3.11.3), forces 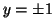 . If
. If
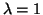 , then we can use Equation 3.11.7 to determine that
, then we can use Equation 3.11.7 to determine that
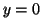 and thus, from Equation 3.11.3,
and thus, from Equation 3.11.3, 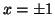 . The
points of intersection are therefore
. The
points of intersection are therefore
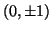 and
and
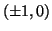 , the same
solutions derived using algebraic substitution.
, the same
solutions derived using algebraic substitution.
no_titleno_title
We want to find the maximum value of
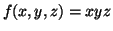 |
(3.11.8) |
subject to the
constraint
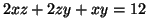 |
(3.11.9) |
(thus,
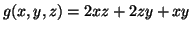 ). In this example, the equations
involve more than two variables so algebraic substitution is not an
option. Thus, it makes sense to use the Lagrange multiplier method here.
We will first set up
the system of equations defined by
). In this example, the equations
involve more than two variables so algebraic substitution is not an
option. Thus, it makes sense to use the Lagrange multiplier method here.
We will first set up
the system of equations defined by
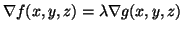 :
:
If we multiply Equation 3.11.10 by 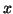 , Equation 3.11.11 by
, Equation 3.11.11 by 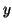 and Equation 3.11.12 by
and Equation 3.11.12 by 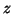 , we have,
, we have,
We can now use these equations to solve for 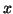 and
and 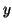 in terms of
in terms of
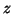 . Using Equations 3.11.13 and 3.11.14 we get,
. Using Equations 3.11.13 and 3.11.14 we get,
Using Equations 3.11.14 and 3.11.15 we get 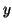 in terms of
in terms of 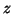 ,
that is,
,
that is,
We can now substitute 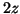 for both
for both 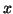 and
and 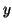 into
Equation 3.11.9 to solve for
into
Equation 3.11.9 to solve for 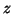 :
:
Using Equations 3.11.16, 3.11.17 and 3.11.18, we
can determine that the only place where both functions intersect is
when 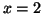 ,
, 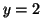 and
and 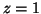 . Thus
. Thus
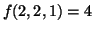 is both the
maximum and minimum from this function subject to the
constraint, Equation 3.11.9.
is both the
maximum and minimum from this function subject to the
constraint, Equation 3.11.9.



Next: Matrix Calculus
Up: Solving Constrained Optimization Problems
Previous: Solving Constrained Optimization Problems
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19