



Next: Taylor series and identifying
Up: Examples of Models
Previous: Microscopic/Probabilistic Behavior
Index
Click for printer friendely version of this HowTo
Non-Linear and Linear DEsno_title
Earlier, we briefly explored the role of a cellular action potential
plays in short term memory. Cells such as neuronal, cardiac and
muscle cells are excitable, i.e. when stimulated with
a subthreshold stimulus, the cell's electrical potential remains
more or less constant. On the other hand, when the cell is stimulated
with a suprathreshold stimulus, the cell's electrical potential
will change dramatically, and over time return to its rest value.
The action potential is a mechanism for cells communicating with
each other. Cellular communication happens when a cell releases a
packet of neurotransmitter that
binds to a receptor on a nearby cell, or when the cell changes its
transmembrane potential and the change is sensed by an adjoining cell.
An example of the first method is a nerve cell talking to another nerve cell
using synaptic coupling. The latter method could take place in heart cells
that are electrically coupled by gap junctions.
What is the minimum complexity of a cell capable of talking (an
excitable cell)? In order for it to be useful in
signaling, it must be able to have
two stable equilibria, rest and excited.
By equilibria, we mean points where the derivative, 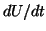 , is zero. By
stable, we mean that when you push the solution to either side
of the equilibrium, the process described by the ode moves the solution
back to the equilibrium.
In order to have two stable
states, the derivative of the current voltage relationship (if we are
considering membrane potential as our means of communication)
must equal zero at three different conditions, two of these zeros will be stable and
one unstable. (See Examples 2.10.1.1, 2.10.1.2 and
2.10.1.3 for illustrations of stable and unstable equilibria.)
Therefore a model, driven by a cubic equation of the form:
, is zero. By
stable, we mean that when you push the solution to either side
of the equilibrium, the process described by the ode moves the solution
back to the equilibrium.
In order to have two stable
states, the derivative of the current voltage relationship (if we are
considering membrane potential as our means of communication)
must equal zero at three different conditions, two of these zeros will be stable and
one unstable. (See Examples 2.10.1.1, 2.10.1.2 and
2.10.1.3 for illustrations of stable and unstable equilibria.)
Therefore a model, driven by a cubic equation of the form:
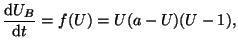 |
(2.8.14) |
where we assume 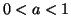 , is required to meet the above conditions.
Equilibria exist when this derivative is zero,
and thus has equilibria,
at
, is required to meet the above conditions.
Equilibria exist when this derivative is zero,
and thus has equilibria,
at  ,
,  and
and 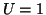 .
A graph of
.
A graph of 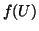 , current, is shown in Figure 2.8.1 and
is called the nullcline. From this, we can graphically explore the
behavior of any ode. An equilibrium exists at each point where the
nullcline crosses the
, current, is shown in Figure 2.8.1 and
is called the nullcline. From this, we can graphically explore the
behavior of any ode. An equilibrium exists at each point where the
nullcline crosses the 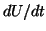 (current)
(current)  axis.
axis.
Figure:
Cubic nullcline for Equation 2.8.14. Here 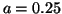 .
.
![\includegraphics[width=3in]{fhn}](img249.png) |
Notice that for 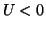 , the nullcline
, the nullcline 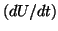 is positive and for
is positive and for 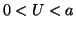 , the derivative is negative. If the solution is sitting at
, the derivative is negative. If the solution is sitting at  and
you push it to the left (say
and
you push it to the left (say 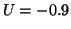 ) then the value of
) then the value of 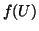 is positive
so that
is positive
so that 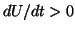 and the solution moves back to
and the solution moves back to  . Similarly, when
you push it to the right (say
. Similarly, when
you push it to the right (say  ), then the value of
), then the value of 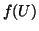 is negative
so that
is negative
so that 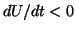 and the solution moves to the left, back to
and the solution moves to the left, back to  .
Thus,
.
Thus,  is a stable
equilibrium. When
is a stable
equilibrium. When 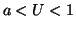 , the derivative is again positive and
thus
, the derivative is again positive and
thus  is an unstable equilibrium. Finally, when
is an unstable equilibrium. Finally, when 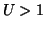 , the
derivative is negative making
, the
derivative is negative making 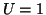 a stable equilibrium.
a stable equilibrium.
The switching nature of this model can be readily demonstrated. Assume
that we are resting at  . Now as you move
. Now as you move 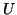 to the right, the derivative
is
to the right, the derivative
is 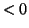 so that if we turn the solution loose, it will migrate back to the
stable equilibrium at
so that if we turn the solution loose, it will migrate back to the
stable equilibrium at  . However, if we continue to push so that
. However, if we continue to push so that 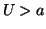 ,
then now
,
then now 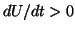 and the solution will continue to the right until it reaches
the point,
and the solution will continue to the right until it reaches
the point, 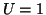 . The point,
. The point, 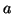 is
called is called the threshold and with this switch, we have a
mechanism for ``talking'', switching from a stable rest (
is
called is called the threshold and with this switch, we have a
mechanism for ``talking'', switching from a stable rest ( ) state to a
stable excitable (
) state to a
stable excitable (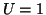 ) state.
) state.
We can add a stimulus function, 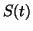 to
to 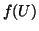 that has magnitude
that has magnitude 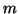 by
simply creating a function that is equal to
by
simply creating a function that is equal to 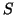 for a given interval
of time. That is:
for a given interval
of time. That is:
 |
(2.8.15) |
where 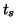 is the duration of the stimulus. This function could be a
reflection of coupling from other cells. For example, a
neurotransmitter opening an excitatory channel transiently. Adding
S(t) to
is the duration of the stimulus. This function could be a
reflection of coupling from other cells. For example, a
neurotransmitter opening an excitatory channel transiently. Adding
S(t) to 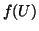 gives us:
gives us:
 |
(2.8.16) |
Depending on the size of 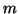 , if we initially start at
, if we initially start at 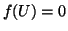 , we
can switch from the rest state to the excitable state as shown
in 2.8.2
, we
can switch from the rest state to the excitable state as shown
in 2.8.2
Here, the stimulus amplitude is 0.25 and the duration of the stimulus is
altered. Starting at the stable equilibrium at 0,0, the potential
increases linearly until the stimulus value returns to zero. By varying
the duration of the stimulus, we can achieve sub-threshold, threshold and
suprathreshold values. Shown are the durations of the stimuli. Note that
for a duration of 1.4, the value of U exceeds the threshold (0.25), at the
end of the stimulus, and thus, rapidly moves toward the higher stable
equilibrium at 1. As the stimulus duration is reduced, the transition
time to the equilibrium at U = 1 is progressively longer until the duration
is 1.02. Now, the value of U at the end of the stimulus is no longer
suprathreshold and the potential decays back to the stable equilibrium
at U = 0.
Figure:
Switching with near threshold stimulation, a = 0.25
![\includegraphics[width=3in]{threshold}](img268.png) .
. |
Now we must determine how the switch can return to a rest state when
it is in an excitable state. Physically, charge is removed from the
cell until it crosses the threshold and then the cell takes over,
lowering its charge until the lower equilibrium has been reached. As
a first attempt at modeling this removal of charge, we could define a
variable  such that:
such that:
 |
(2.8.17) |
The problem, however, with this definition is that  will not
continue to grow when
will not
continue to grow when 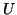 hits the upper equilibrium point. As a
result, the system will never return to the rest state. Thus, we
must add a second term that will allow
hits the upper equilibrium point. As a
result, the system will never return to the rest state. Thus, we
must add a second term that will allow  to grow once
to grow once 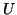 is at the
equilibrium point. In this case we will add a term that causes
exponential decay in the charge:
is at the
equilibrium point. In this case we will add a term that causes
exponential decay in the charge:
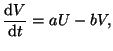 |
(2.8.18) |
where 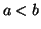 .
From this equation we can see that as
.
From this equation we can see that as 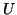 increases, so does
increases, so does 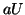 and
thus, so does
and
thus, so does  . Once
. Once 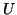 plateaus at the higher equilibrium,
plateaus at the higher equilibrium,  will continue to increase, at slower and slower rates because
will continue to increase, at slower and slower rates because 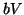 will continue to subtract from
will continue to subtract from 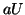 larger and larger amounts, until
larger and larger amounts, until 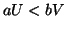 . Once
. Once 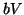 dominates, Equation 2.8.18 will become negative
and
dominates, Equation 2.8.18 will become negative
and  will decrease.
will decrease.
With Equation 2.8.18 for  , our equation defining the
entire cell becomes
, our equation defining the
entire cell becomes
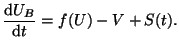 |
(2.8.19) |
By subtracting  from
from 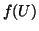 the switch becomes monostable
by
removing two of the equilibria. We can determine the location of the
remaining equilibrium
is determined by examining
when the derivatives for both equations are zero.
the switch becomes monostable
by
removing two of the equilibria. We can determine the location of the
remaining equilibrium
is determined by examining
when the derivatives for both equations are zero.
Since  only plays a significant role after the initial stimulation,
we can omit
only plays a significant role after the initial stimulation,
we can omit 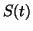 in the following derivations.
First, we will solve
in the following derivations.
First, we will solve
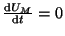 :
:
Now we will solve
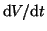 :
:
The result is the strait line in Figure 2.8.3 with a slope of  The intersection gives us a single equilibrium.
The intersection gives us a single equilibrium.
Figure:
Cubic and linear nullcline for the Fitzhugh Nagumo
cell model. When U(t = 0) < 0.25,
the potential collapses because dU/dt < 0.
However, when U(t=0) > 0.25 the potential grows and
produces an action potential.
![\includegraphics[width=3in]{mono_fhn}](img288.png) |
Figure:
A response to sub-thresholdstimulation at 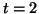 .
The cell potential, U, collapses after the end of the stimulation
pulse because the phase point did not cross the threshold (0.25) marking
the unstable equilibrium 2.8.3 marking the transition from
dU/dt < 0 to dU/dt > 0.
.
The cell potential, U, collapses after the end of the stimulation
pulse because the phase point did not cross the threshold (0.25) marking
the unstable equilibrium 2.8.3 marking the transition from
dU/dt < 0 to dU/dt > 0.
![\includegraphics[width=3in]{fhn_sub}](img289.png) |
Figure:
A response to supra-threshold stimulation at 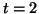 .
In this case, the potential, U, exceedes the threshold, crossing into the
region where dU/dt > 0, and thus accelerates toward the equilibrium at
U = 1. The peak of the action potential never reaches the point where U = 1,
due to the cooling effect reflecting the slow parameter, V.
.
In this case, the potential, U, exceedes the threshold, crossing into the
region where dU/dt > 0, and thus accelerates toward the equilibrium at
U = 1. The peak of the action potential never reaches the point where U = 1,
due to the cooling effect reflecting the slow parameter, V.
![\includegraphics[width=3in]{fhnap}](img290.png) |
In biology, the dynamics of moving from a rest state to an excitable
state is fast because Na channels open quickly. The recovery,
however, is slow because K channels open slowly. We can incorporate
this into our model by including a scaling factor into Equation
2.8.18:
 |
(2.8.20) |
Keep in mind that 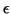 does nothing to alter the equilibrium point
since it simply divides out when solving for it.
does nothing to alter the equilibrium point
since it simply divides out when solving for it.
The switch defined by Equation 2.8.14,
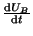 is bistable with
stable equilibria at
is bistable with
stable equilibria at  and
and 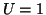 . What we would like to do is
incorperate a variable that will remove charge from the cell during
the excitable stage until the threshold is crossed and the cell and
reset itself to the rest state.
. What we would like to do is
incorperate a variable that will remove charge from the cell during
the excitable stage until the threshold is crossed and the cell and
reset itself to the rest state.

Now - move the slow function linear nullcline to the right where the
equilibrium is unstable. Now the FHN system behaves as an oscillator
as shown in the figure. Same exact model - only a shift in the intersection
of the two nullclines (f(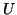 ) = 0, V =
) = 0, V = 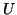 /
/ 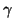
Figure:
Shifted equilibrium to the unstable point
![\includegraphics[width=3in]{nullcline}](img295.png) |
The result is spontaneious oscillation, because the nullclines intersect
at a singular point that is unstable.
Figure:
Oscillation of the FHN system due to the unstable equilibrium
![\includegraphics[width=3in]{fhnosc}](img296.png) |




Next: Taylor series and identifying
Up: Examples of Models
Previous: Microscopic/Probabilistic Behavior
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19