



Next: Setting up Y and
Up: Linear Models
Previous: Linear Models
Index
Click for printer friendely version of this HowTo
General Overview
Let's say that you are studying a type of chicken and you have reason
to believe that its weight will give you some indication of how much
food it will eat in a year (a fairly reasonable thing to suspect).
Ideally we would like to eventually have some sort of function that we
could use hen weight for input and the result would be an estimate
of how much feed we might expect it to consume.
So, you go out and weigh a hen and it turns out to weigh 4.6 units and
consumes 87.1 units. From this single data point, it would be
impossible to tell if a hen that weighed more would eat more (which
would be what we suspected) or would eat less. Thus, we go out an
collect another data point. This time the hen weighs 5.1 units and
eats 93.1 units. If we assumed that there was some sort of linear
relationship between the hen's weight and the amount of feed it
consumes, then we could use the two data points to solve for the
unknown parameters in our model, using them to solve for an intercept
(which we will call 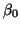 ) a slope (which we will call
) a slope (which we will call 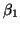 ).
Thus, using the following two equations
).
Thus, using the following two equations
and standard algebraic techniques, we can determine that
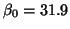 and
and
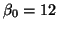 . Thus our model is:
. Thus our model is:
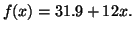 |
(3.13.1) |
Table:
Average body weight  and food consumption
and food consumption  for 50 hens from
each of 10 White Leghorn strains (350-day period).
Source: Plagiarized from Steel, Torrie and Dickey [2]. Data from S. C. King,
Purdue University
for 50 hens from
each of 10 White Leghorn strains (350-day period).
Source: Plagiarized from Steel, Torrie and Dickey [2]. Data from S. C. King,
Purdue University
Body weight,  |
Food Consumption, 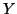 |
| 4.6 |
87.1 |
| 5.1 |
93.1 |
| 4.8 |
89.8 |
| 4.4 |
91.4 |
| 5.9 |
99.5 |
| 4.7 |
92.1 |
| 5.1 |
95.5 |
| 5.2 |
99.3 |
| 4.9 |
93.4 |
| 5.1 |
94.4 |
|
After measuring several more points (Table 3.13.1) you
realize that none of them, except for the first two, which were used
to create the model, fall on the line defined by 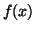 (See Figure 3.13.1).
(See Figure 3.13.1).
Figure:
A plot of the Leghorn data from
Table 3.13.1 with a line drawn using the first two points
to define the slope and the intercept (Equation 3.13.1). Notice how poorly this line
estimates the other data points. For example, with a single
exception, the estimates made by Equation 3.13.1 are
low. Compare this with the graph shown in Figure 3.13.2.
|
|
Figure:
A plot of the Leghorn data from
Table 3.13.1 with a line drawn using Least Squares to
estimate the slope and the intercept. Notice how even though this
line passes through fewer points than Equation 3.13.1,
shown in Figure 3.13.1,
it tends to closer to the majority of the data.
|
|
At this
point we might realize that it was fairly arbitrary to decide to
use the first two points to create our model. We could have used the
second and the third or the fourth and fifth, but using any specify
pair of points to define our model doesn't make it any less arbitrary.
What we would really like to
do is use all of the data that we have collected to create our model.
Since it is obvious that all of the data does not fall on a single
line3.9 we would like to create our model in such a way that the
difference between the points that the model predicts and the
observed data is minimized (see Figure 3.13.2). This section concerns itself with
describing both a method for creating models that achieve this called
Least Squares, and a
means to evaluate the the properties of these models. This method works
well with a wide range of data (not just simple 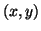 pairs) and
this will be seen in the examples.3.10
pairs) and
this will be seen in the examples.3.10
Least squares is a method for estimating parameters for linear
functions (or, in more technical jargon, functions that are linear
with respect to its coefficients3.11) such that they
minimize the sum of squares of differences
between the 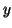 -values of the data points and the corresponding
-values of the data points and the corresponding
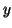 -values of the approximating function.
-values of the approximating function.
We start by considering a linear model of the form
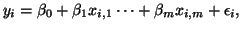 |
(3.13.2) |
where
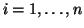 is the number of observations. This system of
is the number of observations. This system of  equations can be written in matrix notation quite concisely with,
equations can be written in matrix notation quite concisely with,
 |
(3.13.3) |
where Y, called the dependent variable, is an
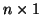 vector of observed measurements3.12,
vector of observed measurements3.12,
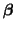 is an
is an
 vector of
unknown model parameters, X, called the independent variables
or the design matrix, is an
vector of
unknown model parameters, X, called the independent variables
or the design matrix, is an
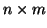 matrix of independent variable values
and
matrix of independent variable values
and
 is the measurement noise.3.13
is the measurement noise.3.13




Next: Setting up Y and
Up: Linear Models
Previous: Linear Models
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
![\includegraphics[width=3in]{leghorn_bad}](img739.png)
![\includegraphics[width=3in]{leghorn_good}](img740.png)