



Next: Properties of Maximum Likelihood
Up: Parameter Estimation Using Maximum
Previous: Overview
Index
Click for printer friendely version of this HowTo
Maximum Likelihood simply uses all those Max/Min strategies that we learned
in high-school calculus and then promptly forgot.
Here's the general strategy in for solving for the value of a
parameter that maximizes the probability of
the data:
- Take the first derivative of the function with respect to the
parameter that you want to solve for.
- Set the derivative equal to zero and attempt to solve for the
parameter.
- If you come up with a single solution, take the second
derivative of the original equation with respect to the parameter,
substitute in your solution for the parameter
and then check to see that it is less than zero. If so, then you have
found the value that maximizes the function. (This has worked in
almost every situation I have encountered.)
- If you come up with multiple solutions, check all the solutions
and check the endpoints of the range as well. (You almost never
have to do this.)
Often times the log of the likelihood function is maximized instead of
just the likelihood function. This is because it is almost easier to
work with the log of the likelihood function than the likelihood
function itself. We can justify this simplification because all probability distributions are non-negative for the domain of
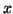 , and the function
, and the function ![$ \log[x]$](img606.png) is an increasing
function in
is an increasing
function in 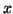 , thus, the solution for the
parameter that maximizes the probability distribution given the data
is the same as
the maximum of the natural logarithm of the distribution given
the data. Also, we'll use the
notation,
, thus, the solution for the
parameter that maximizes the probability distribution given the data
is the same as
the maximum of the natural logarithm of the distribution given
the data. Also, we'll use the
notation,
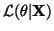 to mean
The maximum with respect to
to mean
The maximum with respect to 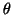 (the parameter that we
want to estimate) of the probability of the
data, X. It is also worth noting that most
statisticians use ``log'' to mean ``natural log'' or ``ln''.
(the parameter that we
want to estimate) of the probability of the
data, X. It is also worth noting that most
statisticians use ``log'' to mean ``natural log'' or ``ln''.
no_titleno_title
From the overview, let's assume that we have X, a vector of  independent
data points,
independent
data points,
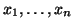 , collected from the same normal distribution where both
, collected from the same normal distribution where both
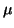 and
and 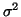 are unknown. Since each element in X is
independent, the probability of the data as a whole is the product of the
probability of each element in X.3.5
are unknown. Since each element in X is
independent, the probability of the data as a whole is the product of the
probability of each element in X.3.5
We will begin by finding an estimate for 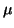 . To do this we will
assume that we know
. To do this we will
assume that we know 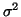 .
.
and
The partial derivative with respect to 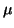 is,
Thus,
is,
Thus,
Verifying that 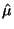 is indeed a maximum requires us to take the
second derivative of Equation 3.9.1 and make sure it is
negative.
is indeed a maximum requires us to take the
second derivative of Equation 3.9.1 and make sure it is
negative.
Thus, since 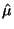 is the only extreme point, is indeed a maximum.
is the only extreme point, is indeed a maximum.
Now we will solve for
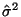 , the MLE
of
, the MLE
of 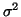 . Starting from Equation 3.9.1 and
substituting in our solution for
. Starting from Equation 3.9.1 and
substituting in our solution for 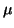 , we can
take the partial derivative with respect to
, we can
take the partial derivative with respect to 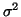 . Thus,
. Thus,
and
To verify that our solution for
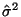 is indeed a maximum,
we have,
is indeed a maximum,
we have,
Substituting in our solution for 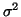 we have,
we have,
and thus, our solution for 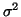 is also a maximum.
is also a maximum.
One final note before we conclude this example. If we had attempted
to solve for the MLE for 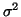 before we solved for
before we solved for 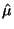 ,
then we would to have ended up with the solution
,
then we would to have ended up with the solution
which still contains the unknown parameter 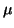 . At this point, we
would have to pause in our derivation of
. At this point, we
would have to pause in our derivation of
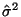 and solve
for
and solve
for 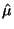 . Once we had a solution for
. Once we had a solution for 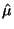 , we would
then substitute it in for
, we would
then substitute it in for 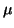 to complete our derivation of
to complete our derivation of
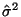 .
.





Next: Properties of Maximum Likelihood
Up: Parameter Estimation Using Maximum
Previous: Overview
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19