|
|



Next: Ordinary Differential Equations
Up: How to create a
Previous: Reverse Engineering
Index
Click for printer friendely version of this HowTo
Some processes are so simple that they can be described in terms of
algebraic equations, either explicitly, or implicitly as the solution
to a differential equation.
Algebraic equations are usually defined by applying some law of physics
like conservation of mass or conservation of momentum or a time or
space dependent equation describing the temporal movement of something.
For example this is an explicit algebraic model:
where 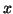 is today's date. An example of an implicit algebraic equation
is the description of the time course of binding of drug to a receptor.
The dynamics is best characterized by a differential equation (equating
changes in the fraction of bound receptors to the difference between
rates of forming and unforming bound receptors) which has a simple
algebraic solution: is today's date. An example of an implicit algebraic equation
is the description of the time course of binding of drug to a receptor.
The dynamics is best characterized by a differential equation (equating
changes in the fraction of bound receptors to the difference between
rates of forming and unforming bound receptors) which has a simple
algebraic solution:
where 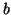 is the fraction of bound receptors, is the fraction of bound receptors, 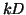 is the rate of making
bound receptors, is the rate of making
bound receptors, 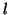 is the rate of unmaking bound receptors and is the rate of unmaking bound receptors and 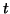 is time.
is time.
Algebraic
models are usually easy to explore because we can simple generate a sequence of
values for the independent variable and plot the resulting values of the
model's dependent variable.



Next: Ordinary Differential Equations
Up: How to create a
Previous: Reverse Engineering
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |