



Next: Reverse Engineering
Up: How to create a
Previous: Introduction
Index
Click for printer friendely version of this HowTo
Figure:
Graphical Taylor analysis, the approximation includes only the linear term
|
|
Often times you are working with awful functions as part
of some analysis. They are impossible to integrate or differentiate or to
find the roots of. As with many things,
the trick is to find a reasonable approximation that is simple enough
to work with. The Taylor Series allows you to do just that. With it
you can decompose any complex function,
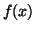 , into an infinite series. Often, a truncated series will be used for
for the analysis. For example, you might end up using only the first
two terms of the series (the linear portion of the approximation). The difference between
the value obtained from the infinite series and the truncated series can
be called "error" or noise.
, into an infinite series. Often, a truncated series will be used for
for the analysis. For example, you might end up using only the first
two terms of the series (the linear portion of the approximation). The difference between
the value obtained from the infinite series and the truncated series can
be called "error" or noise.
The Taylor Series, or Taylor Expansion of any function, 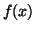 is
defined as:
is
defined as:
The first two terms are the most important
because this is the linear approximation. It says that for any function,
f(x), you can create an approximation of it around any point, 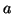 , by
looking at the slope of the function at
, by
looking at the slope of the function at 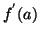 and multiplying it
by the distance between
and multiplying it
by the distance between 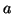 and another point
you want to know something about. It is a straight line approximation, the
value of the function at the point,
and another point
you want to know something about. It is a straight line approximation, the
value of the function at the point,  added to the derivative
added to the derivative
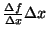 .
.
Approximate Exponentialno_title
To demonstrate the how the Taylor series can generate an approximation
function for 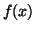 , we will define
, we will define 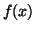 as an exponential
function and create an approximate function around zero. That is, we
will let
as an exponential
function and create an approximate function around zero. That is, we
will let
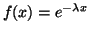 and
and  . Since ,
. Since ,
 , the linear portion of the Taylor expansion is:
, the linear portion of the Taylor expansion is:
If we want
to know
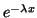 at
at 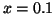 , when
, when
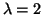 then
then
Compare this approximate answer to the correct answer to 6 decimal places, 0.818731.
Note, if
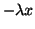 is positive, then the series will
diverge. However,
when the exponent is negative, the series converges. That is, the signs
of each term in the approximation will alternate.
Thus, for some analyses, we can replace
is positive, then the series will
diverge. However,
when the exponent is negative, the series converges. That is, the signs
of each term in the approximation will alternate.
Thus, for some analyses, we can replace
 with
with
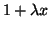 and continue
the analysis.
and continue
the analysis.


Subsections




Next: Reverse Engineering
Up: How to create a
Previous: Introduction
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19