|
|




Next: 2x2 Factorial Interaction Plots
Up: The Joy of Learning.
Previous: .
Index
Click for printer friendely version of this HowTo
Alternative Design Matrices for ANOVA
In most text book discussions of design matrices for ANOVA, they commonly dwell
solely on what is called the over parameterized model and methods
for overcoming its limitations
instead of the model given in
Examples 3.13.2.3 and 3.13.5.4.
This is due primarily to the historical origins of ANOVA and
reverence to the simplifications that assisted solving the computations by
hand. Since we have absolutely no interest in working these problems out by
hand, we have adopted a more modern, and in our opinion, more explicit
design matrix for ANOVA. However, since it is impossible to avoid these
antiquated alternative design matrices and their methods of use, we
will describe them here.
Given the data in mice treatment data in Table 3.13.2, the over
parameterized model is,
where 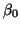 estimates a mean value for all of the data (regardless of the
particular treatment for each sample) and the remaining four parameters
estimate the means of the residuals for each treatment. This model
represents the fact that ANOVA was developed prior to the convenient
access to computers that we have today and it allowed for the
calculations to be done by hand without having to use matrix algebra
explicitly. These methods, however, lack generality and obscure the
question that you want ANOVA to answer. For example, with the mice
data, we ask the question ``Are all the treatments the same?'' With our modern
model, we can easily convert this question into
one we can test by asking, ``Are the means for each treatment the
same?'' Using the over parameterized model we
end up asking the mildly cryptic question, ``Is the variation in
the sample due to variation within treatments or variation between
treatments?'' Both questions eventually will yield the same answer: You
decide which one will be easier to explain
to someone not already steeped in statistical terminology. estimates a mean value for all of the data (regardless of the
particular treatment for each sample) and the remaining four parameters
estimate the means of the residuals for each treatment. This model
represents the fact that ANOVA was developed prior to the convenient
access to computers that we have today and it allowed for the
calculations to be done by hand without having to use matrix algebra
explicitly. These methods, however, lack generality and obscure the
question that you want ANOVA to answer. For example, with the mice
data, we ask the question ``Are all the treatments the same?'' With our modern
model, we can easily convert this question into
one we can test by asking, ``Are the means for each treatment the
same?'' Using the over parameterized model we
end up asking the mildly cryptic question, ``Is the variation in
the sample due to variation within treatments or variation between
treatments?'' Both questions eventually will yield the same answer: You
decide which one will be easier to explain
to someone not already steeped in statistical terminology.
If we are going to use our general hypothesis test (Equation
3.13.21) to answer our question with the
over parameterized model, we must first create the design matrix. Thus, without
displaying the redundant rows, we have:
The problem with this design matrix, however, is that it can not be
used with our hypothesis testing formula due to the fact that
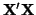 is singular. To work around this problem, statisticians
have come up with three solutions. The first is to remove the last
column in X and modify the parameter vector, is singular. To work around this problem, statisticians
have come up with three solutions. The first is to remove the last
column in X and modify the parameter vector,
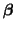 to make up for this change,
the second is to modify X using
what is called to make up for this change,
the second is to modify X using
what is called  -restricted notation, and the third
is to create a generalized inverse of X. Here we will
focus on the first two methods since they are encountered most often
(see Steel, Torrie and Dickey, for examples using the over
parameterized model). -restricted notation, and the third
is to create a generalized inverse of X. Here we will
focus on the first two methods since they are encountered most often
(see Steel, Torrie and Dickey, for examples using the over
parameterized model).
Using the first method we have to make the following changes to the design
matrix and the parameter vector:
Now, if we multiply X and
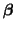 together, we get:
Notice that together, we get:
Notice that
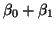 is just the mean of the first
treatment, is just the mean of the first
treatment,
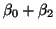 is the mean of the second treatment, and so on.
Thus, after a lot of work modifying X and is the mean of the second treatment, and so on.
Thus, after a lot of work modifying X and
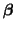 , we are exactly where our modern model began. , we are exactly where our modern model began.
Using  -restricted notation, you allow the independent
variables to take on three different values, 1, 0 and -1, instead of
the binary 1 and 0 used in the other methods. By doing so, we can
indicate membership in the last treatment by using -1 for the other
treatments. This is because we are assuming that the estimates are unbiased
making the sum of the deviations zero. Thus, any particular
deviation can be derived from the others as the negetaive of the sum of the
remaining deviations.
Our design matrix becomes: -restricted notation, you allow the independent
variables to take on three different values, 1, 0 and -1, instead of
the binary 1 and 0 used in the other methods. By doing so, we can
indicate membership in the last treatment by using -1 for the other
treatments. This is because we are assuming that the estimates are unbiased
making the sum of the deviations zero. Thus, any particular
deviation can be derived from the others as the negetaive of the sum of the
remaining deviations.
Our design matrix becomes:
![\begin{displaymath}
{\bf X} =
\left[
\begin{array}{cccc}
1 & 1 & 0 & 0\\
1 & 0 ...
...}
\beta_0\\
\beta_1\\
\beta_2\\
\beta_3
\end{array}\right].
\end{displaymath}](img1239.png)
The results here are similar to the over parameterized model.
It is clear that using a classic ANOVA approach both obscures
the question you are
interested in answering and requires more effort on behalf of
the individual willing to abide by it. These problems also carry over to
ANCOVA whereas our modern model generalizes without any additional effort
(see Example 3.13.5.11). Furthermore, since there it is unessicary to
reparameterize the design matrices involved in ANOVA and ANCOVA, we can
establish the guidline that any design matrix that requires
reparameterization should be a signal that you may be making unrealistic
assumptions about the nature of the data (see Examples 3.13.5.5, 3.13.5.9 and 3.13.5.10). Thus, the
authors are inclined
to recommend using our modern approach to ANOVA.




Next: 2x2 Factorial Interaction Plots
Up: The Joy of Learning.
Previous: .
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |