|
where Z is the valence of the charge carrier and D is the diffusion constant.
Charge carriers are accelerated by the electrical attraction of the carrier within the electric field. As the charge is attracted, things get in the way that result in collisions. After each collision, velocity is lost resulting and is slowly recovered due to the acceleration caused by the attraction of the charge carrier and the potential field. To descirbe this, we start with the force that an unit charge feels within an electric field:
where F is the force, q is the unit charge and E is the electric field. Remember that the electric field, E = dV/dx, is simply the change in potential at a point. Now the attractive force will change the momemtum of a charge carrier either positively (acceleration) or negatively (deceleration). We assume that the drift velocity is
Now define the mobility of the charge, so that the drift velocity is which simply states that in the presence of a spatially uniform electric field, the charge will move with a fixed velocity known as the drift velocity, that is proportional to the charge and inversely proportional to the mass of the charge. Now the current density associated with the flow of charge within an electric field in a solution is: where Z is the valence of the charge carrier, F is the number of coulombs of charge per mole of ion, and [C] is the concentration of charge carriers. But the drift velocity is where
Now we integrate this across the interface (cell membrane) that separates the extracellular fluid from the cytoplasm and have
Einstein showed, in a cute little derivation that where R is the gas constant (8.314 J/K mole at 27 C), and T is the absolute temperature. At 27 C, RT/F = 8.314 * 300 / 96487 = 25.8 mV at 27 C. so for a monovalent cation or anion, the transmembrane potential due to a single charge carrier is:
Next: Cubic Nonlinear ODE Up: Derivations For the Curious Previous: Derivations For the Curious Index Click for printer friendely version of this HowTo Frank Starmer 2004-05-19 |
![\includegraphics[width=3in]{diffusion}](img1083.png)
![$\displaystyle j = -\vert Z\vert D\frac{d[C]}{dt}$](img1084.png)
![\includegraphics[width=3in]{e_field}](img1085.png)
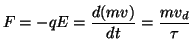
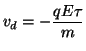
![$\displaystyle -\vert Z\vert D\frac{d[C]}{dx} + \vert Z\vert F[C]\mu E = -D\frac{d[C]}{dx} + F[C]\mu\frac{dV}{dx} = 0$](img1098.png)
![$\displaystyle \int{D\frac{d[C]}{dx}}$](img1099.png)
![$\displaystyle = \int{F[C]\mu\frac{dV}{dx}}$](img1100.png)
![$\displaystyle \int{D\frac{d[C]}{[C]}}$](img1101.png)
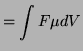
![$\displaystyle = \frac{D}{F\mu} ln\frac{[C_{\textrm{out}}]}{[C_{\textrm{in}}]}$](img1106.png)
![$\displaystyle V_{\textrm{membrane}}(mV) = \frac{RT}{F} \frac{[C_{\textrm{out}}]}{[C_{\textrm{in}}]} = 25.8 ln\frac{[C_{\textrm{out}}]}{[C_{\textrm{in}}]}$](img1108.png)