


Next: Generating Random Variables From
Up: Generating Random Variables
Previous: Sampling From a Distribution
Index
Click for printer friendely version of this HowTo
There are two primary methods for generating normally distributed
random variables. The first method relies on the central limit theorem
which states that if E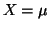 and Var
and Var
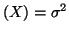 , then for
independent and identically distributed samples from any distribution
, then for
independent and identically distributed samples from any distribution
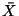 has an approximate
has an approximate
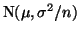 distribution, where
distribution, where 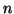 is the sample size. The utility in this first method is that it
is very easy to remember off the top of your head and is relatively
easy to compute with a computer.
is the sample size. The utility in this first method is that it
is very easy to remember off the top of your head and is relatively
easy to compute with a computer.
The second method uses a direct transformation, and, while being just
as easy to compute using a computer, is a little tricky to
remember. This method is called the Box-Muller algorithm. The steps
involved are:
- Generate to independent uniform(0,1) variables,
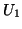 ,
, 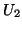 .
.
- Let
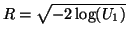 and
and
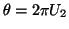
- Let
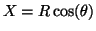 and
and
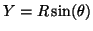 .
.
where 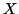 and
and 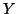 are independent normal(0,1) random variables. See
Appendix A.2 for an Octave program that implements
this algorithm.
are independent normal(0,1) random variables. See
Appendix A.2 for an Octave program that implements
this algorithm.



Next: Generating Random Variables From
Up: Generating Random Variables
Previous: Sampling From a Distribution
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19