|
|




Next: Numerical Approximations of Power
Up: How to ask questions
Previous: Comparing Two Samples: Classifying
Index
Click for printer friendely version of this HowTo
Power is a term that is used quite frequently to describe
statistical tests. As is often the case, the word has a rather
specific definition which we will attempt to describe here. Due to
their close relation
to the definition of power, we will also briefly describe the various
types of errors that statistical tests can make. Thus,
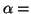 the probability you will reject the probability you will reject 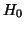 when it is
true. This type of error is called Type I Error. when it is
true. This type of error is called Type I Error.
 the probability you will accept the probability you will accept 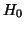 when it
false. This type of error is called Type II Error. when it
false. This type of error is called Type II Error.
- Power
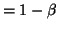 , the probability the test will
reject , the probability the test will
reject 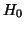 when it is false.
Thus, the more power, the higher probability of
correctly rejecting when it is false.
Thus, the more power, the higher probability of
correctly rejecting 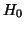 . .
You can increase power by increasing the sample size,  , for the test.
This is because the larger sample size will decrease the variance of
the estimated parameters. For example, consider , for the test.
This is because the larger sample size will decrease the variance of
the estimated parameters. For example, consider 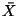 as an
estimate of as an
estimate of 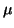 .
By the central limit theorem, the variance of .
By the central limit theorem, the variance of 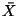 , where
E , where
E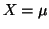 and Var and Var
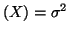 for
independent and identically distributed samples from any
distribution, is approximately for
independent and identically distributed samples from any
distribution, is approximately
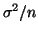 , which gets smaller as , which gets smaller as  gets larger.
gets larger.
An example of this is shown in Figures 3.3.1 and 3.3.2.
Figure:
The predicted distribution of 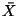 given by the null hypothesis, given by the null hypothesis,
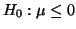 , is depicted in the top graph.
The bottom graph shows the true distribution of , is depicted in the top graph.
The bottom graph shows the true distribution of 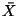 , since , since 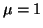 . With the current sample
size, the variation in . With the current sample
size, the variation in 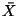 , our estimator for , our estimator for 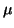 , is great
enough to make it more than likely that we well fail to reject , is great
enough to make it more than likely that we well fail to reject 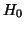 even
though it is false. even
though it is false.
![\includegraphics[width=3in]{power_1}](img503.png) |
Figure:
The predicted distribution of 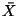 given by the hull hypothesis, given by the hull hypothesis,
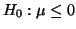 , is shown in the top graph. The bottom graph depicts the
true distribution of , is shown in the top graph. The bottom graph depicts the
true distribution of 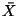 , since , since 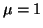 . However, compared
with Figure 3.3.1,
the sample size has been increased enough to reduce the variation in
the parameter estimate by one half. This makes it more likely that
our test will reject . However, compared
with Figure 3.3.1,
the sample size has been increased enough to reduce the variation in
the parameter estimate by one half. This makes it more likely that
our test will reject 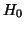 , and thus, the test has more power. , and thus, the test has more power.
![\includegraphics[width=3in]{power_2}](img504.png) |
Subsections




Next: Numerical Approximations of Power
Up: How to ask questions
Previous: Comparing Two Samples: Classifying
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |