|
The Cardiac Vulnerable Period:
a function of conduction velocity and
the spatial gradient of excitability
When extra stimuli are used to probe the excitability of the heart in
the interval between
heart beats, there is a window of time, during which life threatening
arrhythmias can be reproducible induced. This window is called the vulnerable
period or the vulnerable window. The VP is readily demonstrated with any
model of an excitable medium, and shown here are measures of the VP when
the velocity of the initial wave is varied.
Here are simulations based on the guarded receptor model of drug binding
to sodium channels and the Beeler Reuter cardiac model. (Some will be
critical of usint the BR model. My defence is that it is simple, and thus
computationally fast; the VP is generic and therefore can be demonstrated
with any model of an excitable medium; and there are no "complete" models
of the cardiac electrophysiology. "More realistic" models are often
mixtures of less realistic models, combined with empirical adjustments used
to improve the quality of the fit. This, in my opinion, does not qualify
as a "more realistic" model).
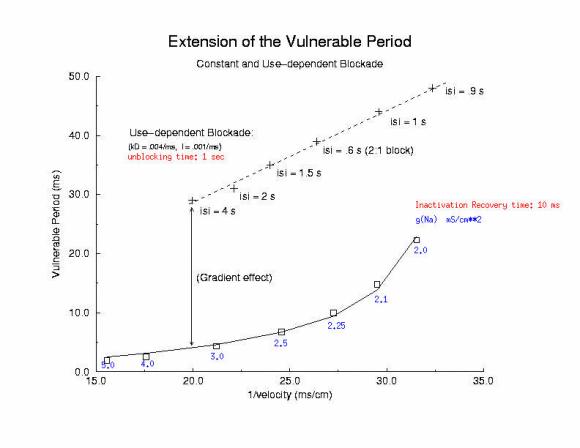
Note, however, a small puzzle with these results: there appear to be
two VPs associated with a single value of the velocity of the conditioning
wave. Early models of the VP were based on the time required for a critical
point to cross the suprathreshold region of the s2 stimulation field - so
VP = L/v where L is the length of the field and v is the velocity of the
conditioning (s1) wave.
Here we see that when the conduction velocity is slowed by
simply reducing the maximum
sodium conductance, gNa, the VP is shorter (blue line)
than when the conduction velocity
is slowed by use-dependent drug (red line).
This is only possible, from the biophysical perspective, if the electrode
length, L, were increased by an amount dependent on the dynamics of the
drug-channel interactions.
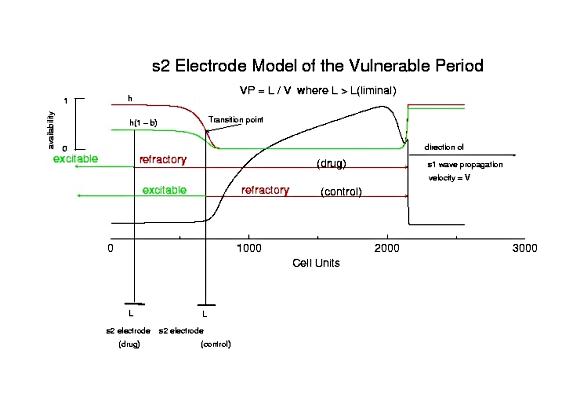
Here is a model of the vulnerabible period. The key feature is to note that
there is a bifurcation in the cellular excitability that separates refractory
states from excitable states (labeled Transition point). Media to the left
of this is excitable and supports wave formation and propagation. Media to
the right of this point is inexcitable, and forming waves collapse.
The VP based on this model is determined by the length of time the
transition point requires to cross the electrode field: VP = L/v . However,
numerical studies and clinical studies indicate that long time constant
drugs may alter the VP, perhaps at the same velocity.
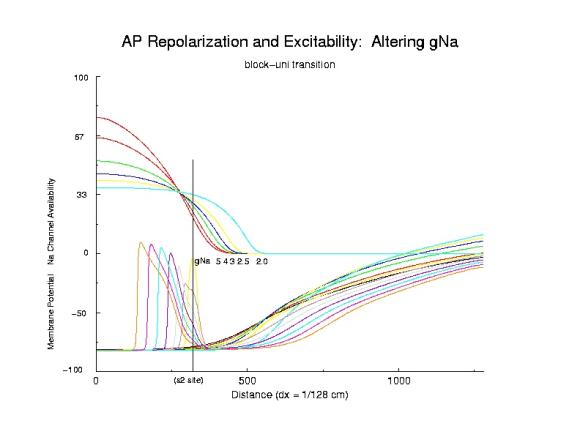
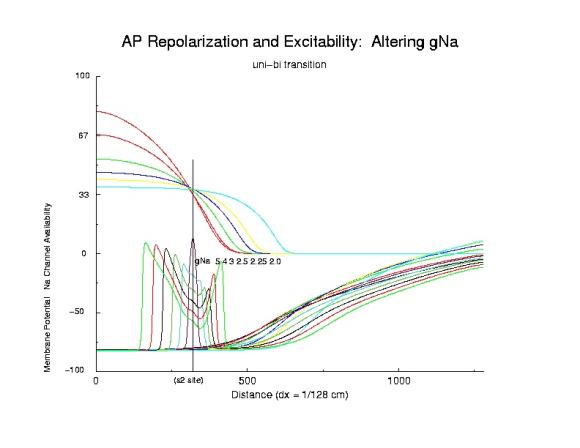
Here I demonstrate the critical nature of the bifurcation point. Plotted
are action potentials (at 5 ms intervals after s2 stimulation)
and Na channel availability gNa*h*j*(1-b) (approximating
the excitability of a cell>. In addition, a drug that binds to the
inactivated state of the No channel is included. Shown are the Na
availability curves for different unbinding rates (the slowest, .0001/ms
and the fasted, 0.1/ms) which demonstrate how the
spatial gradient of excitability
can be altered at the block-uni transition and the uni-bidirectional
propagation interface. Note that the critical point is to the left
of the s2 stimulus site (show is also the potential distribution due to the
injected stimulus current). That all the availability curves intersect in
the same region is evidemce that availability is a major determinant of
the VP. Note that the right of the s2 stimulus site has fewer Na channels
available for activation and results in unidirectional propagation.

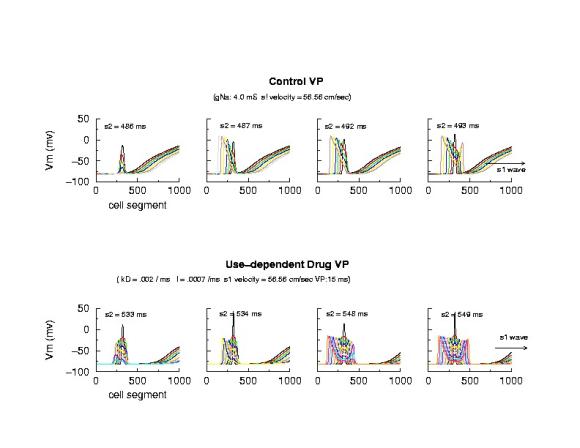
VP: Control and Slowly Unbinding Use-dependent Drug
Note in the figure below that the VP for control and drug is quite
different when the conditioning velocity is the same - thus the above model
needs to incorporate a feature that links blockade dynamics with the VP.
VP Boundaries and Na Channel Availability
Shown here are comparable profiles of recovery of Na channel availability
under drug-free conditions.
Using the Beeler Reuter model (all cardiac and neuronal models display this
behavior), I plotted gna*h*j and normalized gna = 5 to 1. Note the steep
gradient of excitability recovery which is determined by the inactivated to
non-inactivated rate for the Na channel - typically at -80 mV about 1- 10 ms.
Note the short distance between the repolarization
tail of the conditioning action potential and the VP boundary. This is a
measure of the refractory interval and is relatively small compared with the
drug figure below.
The critical point is to the left of the stimulation site so that a collapsing
antegrade wave is assured. As the stimulus field collapses, following
termination of the stimulus pulse, it also propagates
in a decremental manner slowly in the retrograde
direction and as it approaches the critical point, propagation becomes
incremental. The action potential traces at the bottom are at successive
5 ms intervals and clear show the dynamics of front formation and collapse.
Shown here is the other boundary of the VP. Note that the transition point is
virtually superimposed over the electrode site so that the initial moments of
propagation encounter marginally excitable media in both antegrade and
retrograde directions leading to bidirectional propagation.
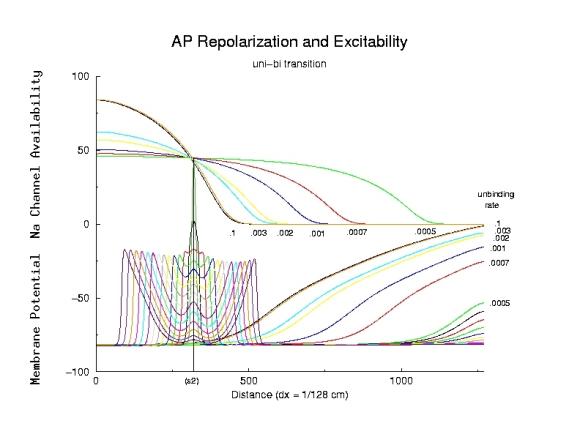
With a use-dependent Na channel blocker (class 1 antiarrhythmic) a significant
number of channels are blocked during the conditioning action potential.
Following repolarization, the drug slowly unbinds from the channel - but
this slow process extends the spatial excitability gradient as seen below.
Note that the refractory period is dramatically increased, a result of
reduced excitability secondary to channel blockade.

Here the s2 stimulus is activated at the boundary that separates unidirectional
conduction from bidirectional conduction.
The lower traces (action potential) are shown for each unbinding rate as
indicated on the right. For l = .0005 / ms, there are a series of
traces, for each 5 ms following s2 stimulation. The dynamics of wave front
formation and collapse are readily appreciated. Note the initial decremental
propagation of the antegrade wave, as the initial front propagates into
marginally excitable media. Note that the decremental conduction is reversed
at approximatly the same place as the critical transition point at the time
of s2 stimulation.
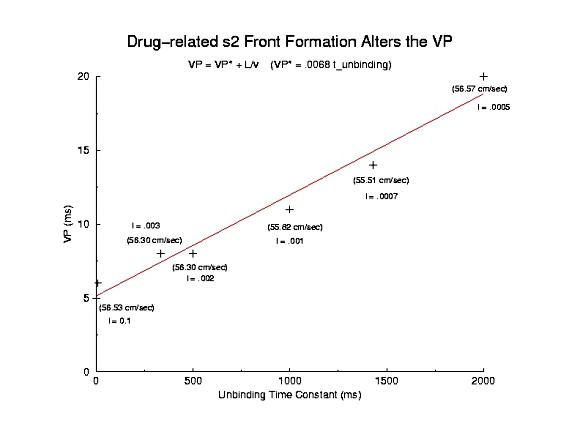
Displayed below is a plot of the VP for drugs with different unbinding rates.
The measurement was made after a single conditioning pulse, in order to
have comparable measurement by eliminating variations in the s1 velocity
(i.e. no use-dependent drug accumulation). Shown is the conduction velocity
and unbinding rate for drugs with time constants ranging from 10 ms to 2 sec.
The linear relationship between VP and time constant is consistent with
the above figures which portray the recovery of channel availability, in this
case recovery is dominated by the drug unbinding process. Because recovery
dynamics is dominated by the drug unbinding time constant, I hypothesize that
the dynamics of wave-front formation is altered in proportion to the time
constant of unbinding. The model for the VP is extended to now include
2 components:
a conditioning velocity component
a drug unbinding component.
The final relationship is VP = alpha/l + L/v where alpha is an arbitrary
constant reflecting front formation processes in the presence of a dynamic
blockade process, l is the unbinding time constant, L is the electrode length
and v is the s1 conditioning velocity.
Copyright 2001 C. Frank Starmer
|